Sudoku strategies explained with graphics

Strategies


Overview Singles Naked Pairs Naked Triples Hidden Pairs Hidden Triples Naked Quads Hidden Quads Pointing Pair Pointing Triple Box Reduction X-Wing Finned X-Wing Sashimi Finned X-Wing Franken X-Wing Finned Mutant X-Wing Skyscraper Chute Remote Pairs Simple Coloring Y-Wing W-Wing Swordfish Finned Swordfish Sashimi Finned Swordfish Franken Swordfish Mutant Swordfish Finned Mutant Swordfish Sashimi Finned Mutant Swordfish Sue De Coq XYZ-Wing X-Cycle Bi-Value Universal Grave XY-Chain 3D Medusa Jellyfish Jellyfish Jellyfish Avoidable Rectangle Unique Rectangle Hidden Unique Rectangle WXYZ-Wing Firework Subset Exclusion Empty Rectangle Sue De Coq Extended SK Loop Exocet Almost Locked Sets Alternating Inference Chain Digit Forcing Chains Nishio Forcing Chains Cell Forcing Chains Unit Forcing Chains Almost Locked Sets Forcing Chain Death Blossom Pattern Overlay Bowman Bingo



❮ Previous Next ❯

X-Cycle


In this strategy we build loops by alternately chaining Weak Links and Strong Links (also see note at the bottom of this page). Such a loop can be read in both directions; whichever the direction, a Strong Link remains a Strong Link and a Weak Link remains a Weak Link.

There are three kinds of X-Cycles:

  • NICE LOOP : all along the loop Weak Links and Strong Links perfectly alternate
  • DISCONTINUOUS LOOP WITH WEAK LINKS : we start from a Cell with a Weak Link and we close the loop on that same Cell with another Weak Link; for the rest, the loop is "nice" (Weak Links and Strong Links perfectly alternate)
  • DISCONTINUOUS LOOP WITH STRONG LINKS : we start from a Cell with a Strong Link and we close the loop on that same Cell with another Strong Link; for the rest, the loop is also "nice".


If we can build a NICE LOOP, then each Weak Link starts on the end Cell of a Strong Link. Because of the definition of a Strong Link the candidate in the Cell at the end of the Strong Link must be the solution. As each Weak Link starts on a Cell that is the end of a Strong Link (whichever the direction used to read the loop), one of the Cells in the Weak Link has the candidate as its solution. Hence the candidate can not be the solution for any Cell that sees both ends of the Weak Link.

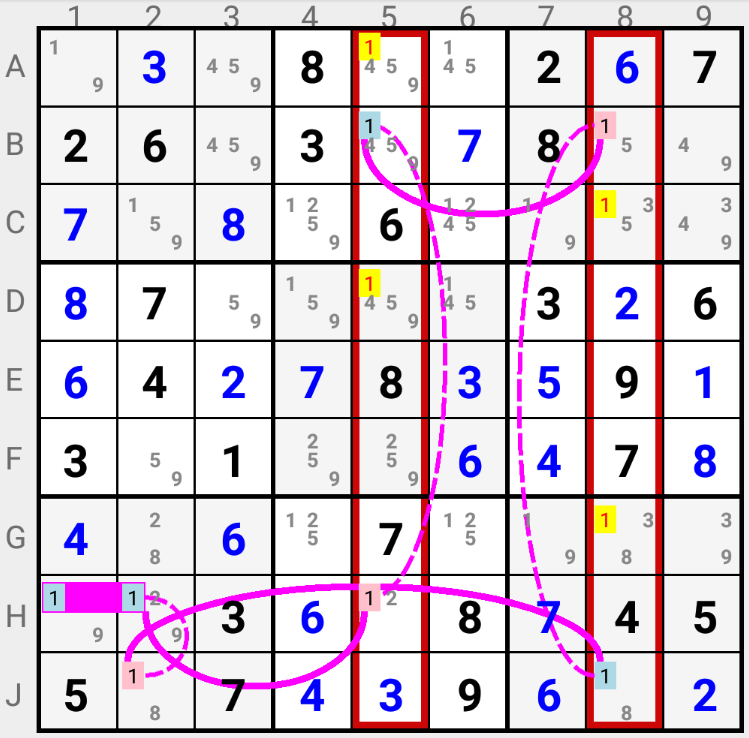
X-Cycle with a Nice Loop

In the above example weak links in Columns "5" and "8" allow eliminating some candidates 1 in these columns. The weak link in Square "7" does not allow any elimination because there are no candidates 1 in cells outside of the weak link.
Note the multicell node in [H1, H2]:

  • if candidate 1 is the solution in H5, then it can not be the solution in H1, nor in H2 (i.e. if H5(1) is ON, then [H1, H2](1) is OFF)
  • if candidate 1 is the solution in H1 or H2, then it can not be the solution in H5 (i.e. if [H1, H2](1) is ON, then H5(1) is OFF)
  • if candidate 1 is the solution in J2, then it can not be the solution in H1, nor in H2 (i.e. if J2(1) is ON, then [H1, H2](1) is OFF)
  • if candidate 1 is the solution in H1 or H2, then it can not be the solution in J2 (i.e. if [H1, H2](1) is ON, then J2(1) is OFF)



When we build a DISCONTINUOUS LOOP WITH WEAK LINKS, the Cell where the discontinuity occurs simultaneously sees the starting Cell of a Strong Link and the ending Cell of a Strong Link (whichever the direction used to read the loop). Because the candidate in the ending Cell of a Strong Link must be the solution for that Cell, the Cell where the discontinuity occurs always "sees" a Cell where the candidate is the solution. Hence the candidate in that Cell can not be the solution for that Cell.

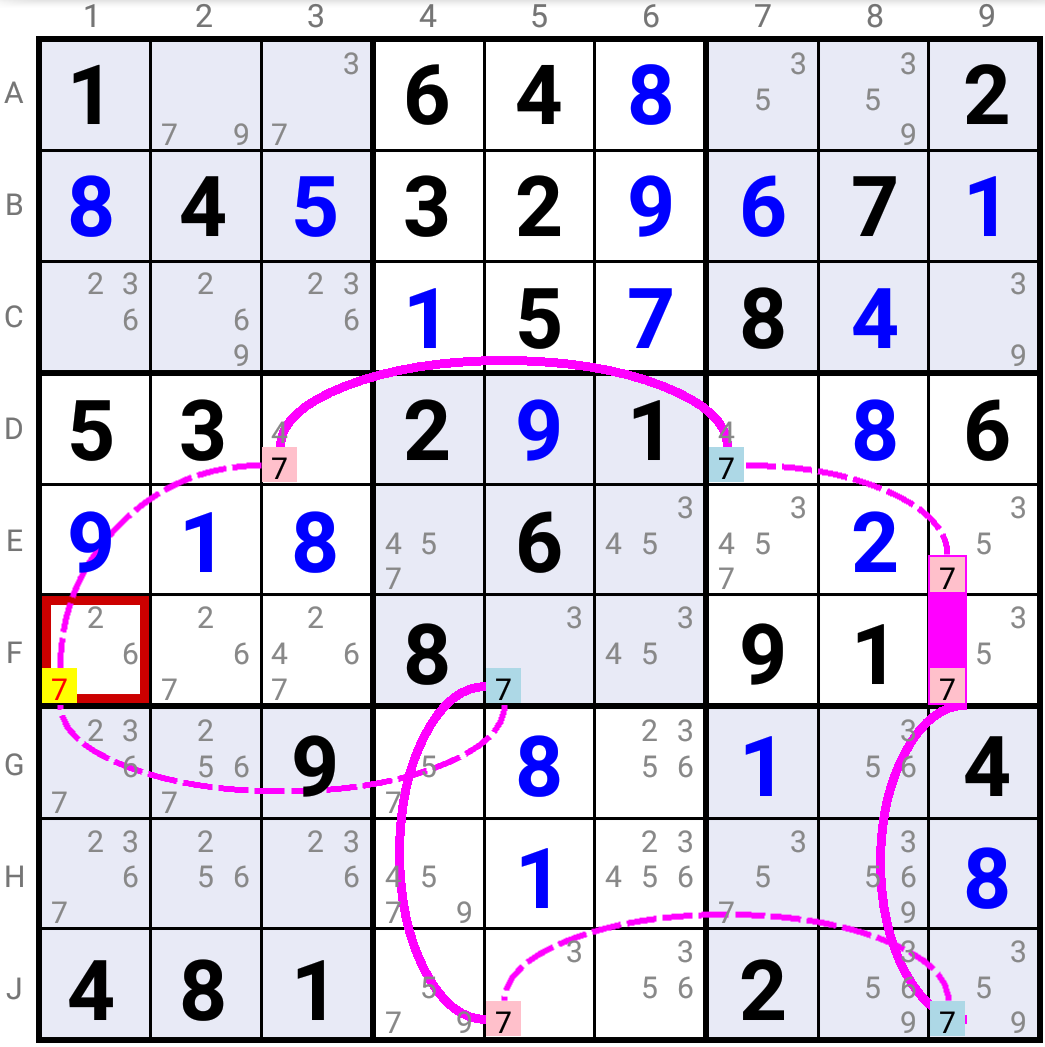
X-Cycle with a Weak Links discontinuity

In this example if you read the loop starting in D3 and progressing through D7, then F5 is the end cell of a Strong Link: hence candidate 7 is the solution in F5 and candidate 7 is thus eliminated from F1.
If you read the loop starting in F5 and progressing through J5, then D3 is the end of a Strong Link: hence candidate 7 is the solution in D3, and candidate 7 is thus eliminated from F1.



When we build a DISCONTINUOUS LOOP WITH STRONG LINKS, the Cell where the discontinuity occurs simultaneously is the starting Cell of a Strong Link and the ending Cell of another Strong Link (whichever the direction used to read the loop). Because the candidate in the ending Cell of a Strong Link must be the solution for that Cell, the Cell where the discontinuity occurs must have the candidate as its solution.

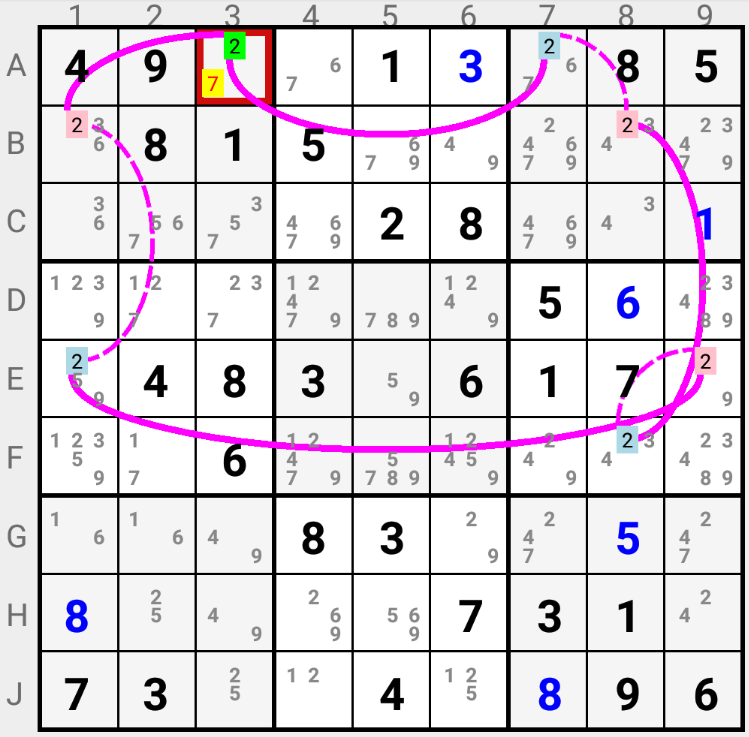
X-Cycle with a Strong Links discontinuity

In this example candidate 2 in A3 is the end Cell of either the Strong Link between B1 and A3, or the Strong Link between A7 and A3, depending on the direction used to read the loop.




NB: more formally, a Strong Link is the relationship that exists between two Cells in a region (Row, Column or Square) when these two Cells are the only Cells in that region that contain a particular candidate: if the candidate is not the solution for the first Cell, then it must be the solution for the second Cell, and vice-versa.
However, in the Chaining Strategies, we consider Strong Links as links going from a Cell or a group of Cells where we assert the candidate is not the solution (we say the candidate is in the "OFF" state) to a Cell or a group of Cells where it then must be the solution (we say the candidate is in the "ON" state).
If we consider a Bi-Value Cell, asserting that one of its candidates is not the solution implies that the other candidate must be the solution. Hence there also exists a Strong Link between the two candidates of a "Bi-Value" Cell.

A Weak Link as a link going from a Cell/group of Cells where the candidate is "ON" to a Cell/group of Cells where it is "OFF".


You can practice this strategy by installing the SudokuCoach application on your Android™ device.

Get it on Google Play

❮ Previous Next ❯