Mutant Swordfish
The basic Swordfish strategy is based on three Rows with constraints on three Columns, or vice-versa. In the Mutant Swordfish strategy, we still use constraints on three regions. However the regions must not be all of the same kind; they can represent various combinations of Rows, Columns and Squares, leading to the different types of Mutant Swordfishes. The Mutant Swordfish strategies regroup all combinations of three regions that lead to eliminations, except those used in the basic Swordfish and in the Franken Swordfish.
RCBRCB Mutant Swordfish
The RCBRCB Mutant Swordfish is based on constraints between one Row, one Column and one Square. It leads to potential eliminations in one Row, one Column and one Square.
If, for a particular candidate, one can find a Row and a Column
- where this candidate is not present in the cell at the intersection of the Row and the Column
- but where this candidate is present in the Square containing this intersection (let us call this Square "Square-3")
- and where the candidate is present in only one Cell outside of Square-3 (let us call it "Cell-1" in the Column and "Cell-2" in the Row),
then these Cells form a pattern called a RCBRCB Mutant Swordfish. Such a pattern allows eliminating the Candidate from all Cells in "Row-1", "Column-2" and "Square-3", except from the Cells that are included in the RCBRCB Mutant Swordfish itself.

In this example the RCBRCB Mutant Swordfish is based on candidate 1 and it is made of Row "D", Column "9" and Square "7".
If candidate 1 is the solution in D2, then candidate 1 can be eliminated in Column "2" (in particular in E2) and it is the solution in G3 which eliminates it in Row "G" (in particular in G7 and G8).
If candidate 1 is the solution in either D7, or D8, then it is the solution in G9 and candidate 1 can be eliminated in Row "G" (in particular in G7 and G8); this implies that candidate 1 is the solution in H2, which eliminates it in Column "2" (in particular in E2).
Whichever the solution for candidate 1 in Row "D", it can never be the solution in E2, G7 or G8.
RCCRBB Mutant Swordfish
The RCCRBB Mutant Swordfish is based on constraints between one Row and two Columns. It leads to potential eliminations in one Row and two Squares.
Let us define a band as a group of three Squares that are aligned either horizontally, or vertically. E.g. Squares "1", "2" and "3" form a band; squares "1", "4" and "7" form another band.
If you can find two Columns (that we call Column-1 and Column-2) in two different bands that each contain a particular Candidate in maximum three Cells that also belong to the same Rows,
if two of these Cells in Column-1 share a common Square that we call Square-1 and the corresponding Cells in Column-2 share a Square-2,
if the third Row (that we call Row-3) of the band including Square-1 and Square-2 contains the Candidate in Square-1 and in Square-2, but does not contain it in the third Square of that band,
then the Cells containing the Candidate form a pattern called a RCCRBB Mutant Swordfish. Such a pattern allows eliminating the Candidate from all Cells in Square-1 and in Square-2, plus in the Row including the third Cell of the Columns, except in the Cells that are included in the RCCRBB Mutant Swordfish itself.
The candidate must not be present in all Cells of Row-3, as long as it is present at least once in each of the portions of Row-3 inside Square-1 and Square-2.
The reasoning is also applicable when you replace "Column" by "Row" and "Row" by "Column".
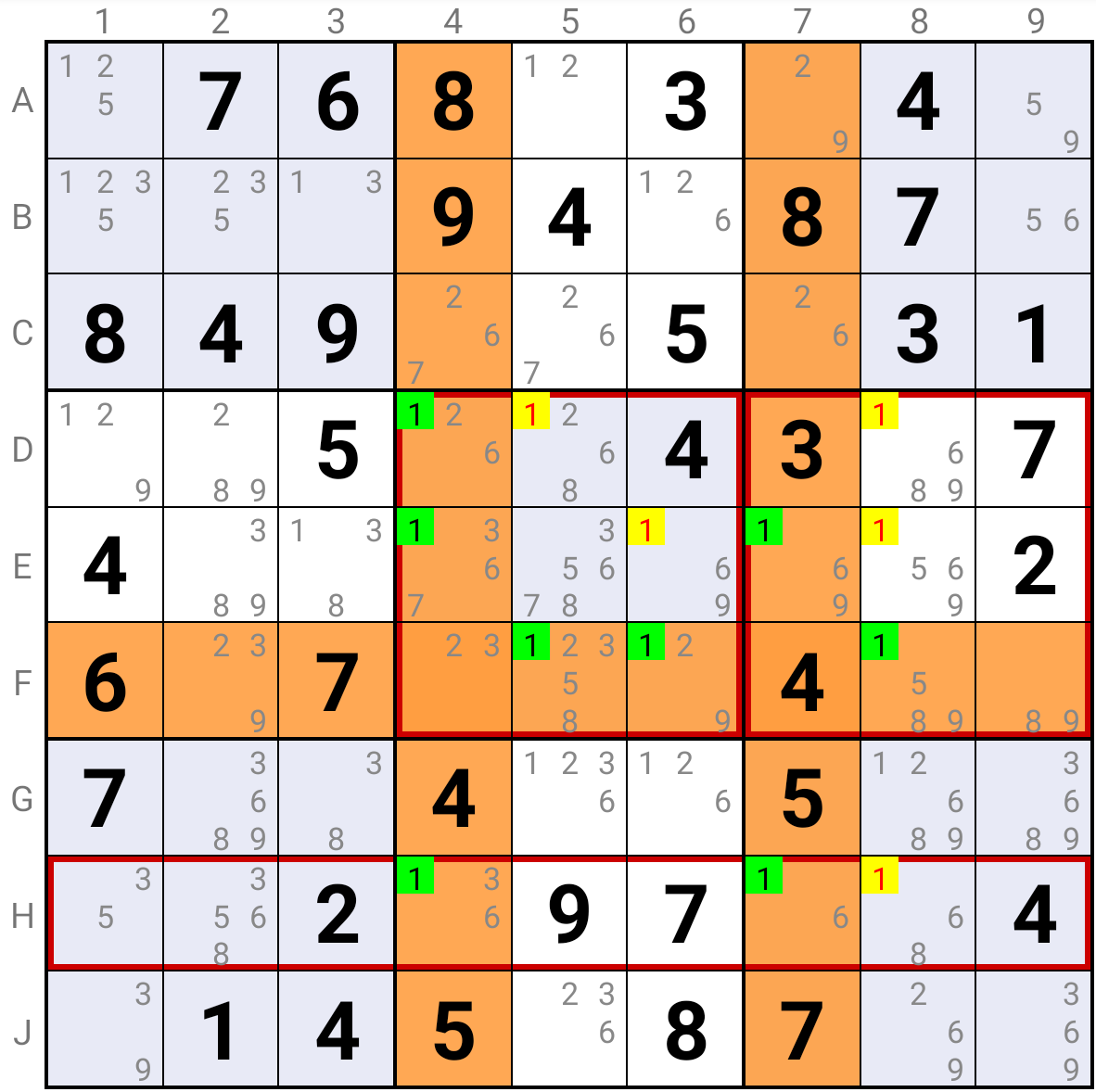
In this example the RCCRBB Mutant Swordfish is based on candidate 1 and it is made of Row "F", Column "4" and Column "7".
If candidate 1 is the solution in H4, then it is the solution in E7 and in F5 or F6, with the highlighted eliminations.
If candidate 1 is the solution in H7, then it is the solution in D4 or E4 and in F8, with the same eliminations.
If candidate 1 is the solution in D4 or E4, then it is the solution in F8 and in H7, with the same eliminations.
If candidate 1 is the solution in F5 or F6, then it is the solution in H4 and in E7, with the same eliminations.
If candidate 1 is the solution in E7, then it is the solution in F5 or F6 and in H4, with the same eliminations.
If candidate 1 is the solution in F8, then it is the solution in H7 and in D4 or E4, with the same eliminations.
Whichever the solution for candidate 1 in the fish, it can never be the solution in D5, E6, D8, E8 or H8.
RBBRCC Mutant Swordfish
The RBBRCC Mutant Swordfish is based on constraints between one Row and two Squares. It leads to potential eliminations in one Row and two Columns. It is the inverse of the RCCRBB Mutant Swordfish.
If you can find a Row (called Row-1) where the Candidate is present in only two Cells (belonging to Column-1 and Column-2) in different Squares,
If you can find two Squares (that we call Square-1 and Square-2)
- that do not overlap Row-1,
- that contain two Rows that each contain the Candidate only in Column-1 and Column-2,
- where the Candidate is present in the third Row (called Row-3),
then the Cells containing the Candidate form a pattern called a RBBRCC Mutant Swordfish. Such a pattern allows eliminating the Candidate from all Cells in Column-1, Column-2 and Row-3, except in the Cells that are included in the RBBRCC Mutant Swordfish itself. The candidate must not be present in all Cells of the RBBRCC Mutant Swordfish, as long as all allowed combinations of the candidate present in the pattern result in the candidate being the solution in each region (Row-1, Square-1 and Square-2) of the pattern.
The reasoning is also applicable when you replace "Column" by "Row" and "Row" by "Column".
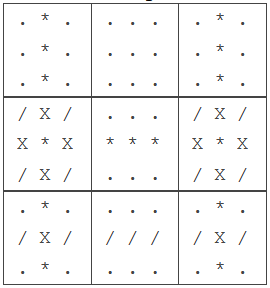
"X" indicates a Cell where the Candidate is present.
"/" indicates a Cell where the Candidate is not present.
"*" indicates a Cell in which the Candidate can be eliminated.
You can practice this strategy by installing the SudokuCoach application on your Android™ device.
