Let us define an "Almost Locked Set" ("ALS" in short) as a set of n Cells in the same region (Row, Column or Square) containing in total exactly (n+1) Candidates: eg a "Bi-Value" Cell or two "Bi-Value" Cells with a common Candidate.

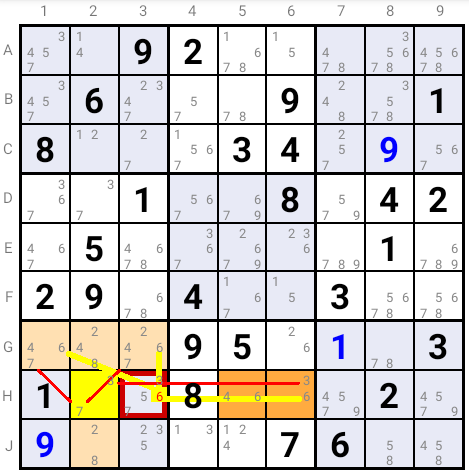
The combinations of the Candidates of two cells can not duplicate any combination of the Candidates of the "ALS" they both entirely see.

Indeed, if such a combination were the solution for these two Cells, then the two corresponding Candidates would be eliminated from the "ALS", which would then only contain (n-1) Candidates in total for n Cells.

In the example if Candidate 6 were the solution in H3, then

• Candidate 3 as solution in H2 would empty Cell H6 and leave only one candidate in ALS {H5, H6}
• Candidate 7 as solution in H2 would leave only Candidates 2, 4 and 8 in ALS {G1, G2, G3, J2}

which is not possible.

You can practice this strategy by installing the SudokuCoach application on your Android™ device.