The first step consists in identifying the following Givens signature:

• Givens in four Cells in different Squares forming the corners of a rectangle (these Cells are called pivots)

If the Givens signature is confirmed, further requirements apply to the Squares containing the pivots:

1. the Squares that are located in the same
   Banda group of three Squares that are aligned either horizontally, or vertically
   have a pair of Candidates in common (we call it an outer link),
2. inside these Squares the two Cells in the mini-Row containing the pivot together contain only four Candidates (these two Cells form what we call a Node),
3. the two Cells in the mini-Column containing the pivot also together contain only four Candidates (these two Cells also form a Node),
4. this mini-Row and this mini-Column have two Candidates in common which are not part of the outer links; these two Candidates form what we call an inner link

When all these requirements are met, then the following eliminations can be made:

1. in the Row or Column containing two pivots, all Candidates of the outer link can be eliminated outside the Squares containing the pivots
2. in a Square containing a pivot, all Candidates of the inner link can be eliminated outside the mini-Row and the mini-Column

Indeed,

1. if 2 Candidates of an inner link are true in a Node in a particular Square, then the other Node in the same Square must contain the 2 Candidates of the outer link in this Node, which eliminates them from the linked Square and forces the 2 Candidates of the inner link of this Square to be true in its other Node; and this process repeats itself until the loop is closed
2. if 1 Candidate of an inner link is true in a Node in a particular Square, then the other Candidate of the inner link is true in the other Node of the Square. The other Cell of these Nodes contains thus 1 Candidate of the associated outer link, which is eliminated from the Node in the related Square. This Node must now contain the other Candidate of this outer link and 1 Candidate of the inner link in this second Square. And this process repeats itself until the loop is closed
3. if 0 Candidates of an inner link are true in a Node in a particular Square, then the 2 Candidates of the outer link in this Node are true. This eliminates them from the corresponding Node in the related Square, in which the 2 Candidates of the inner link must then be true and we are in the same situation as above.

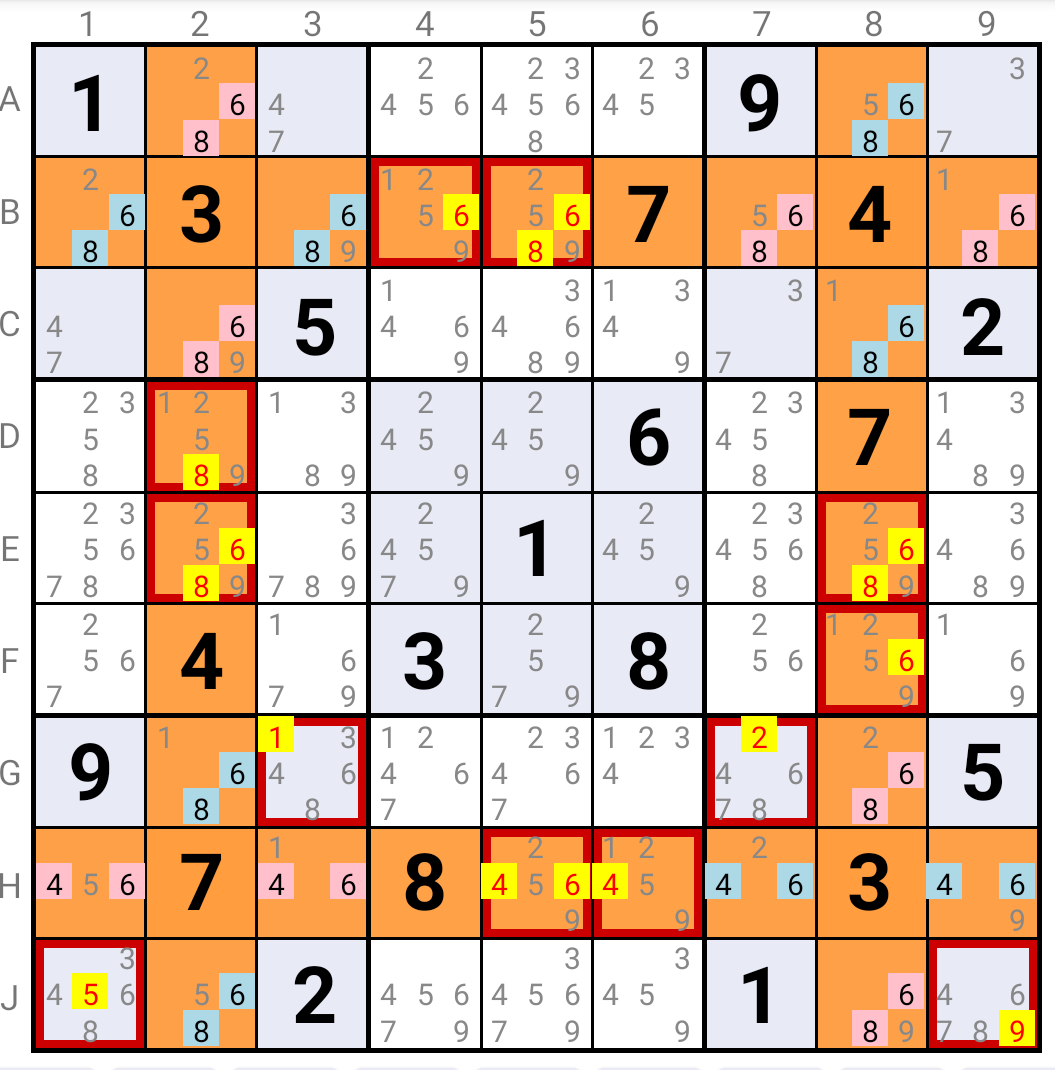
In this example, if we assume that Candidates 6 and 8 are true in B1 and B3,
then Candidates 2 and 9 are true in A2 and C2, and 5 and 1 are true in B7 and B9, and Candidates 6 and 8 are true in A8 and C8
which implies that Candidates 2 and 9 are true in G8 and J8, and Candidates 4 and 6 are true in H7 and H9,
which in turn implies that Candidates 1 and 5 are true in H1 and H3, and Candidates 6 and 8 are true in G2 and J2,
The loop is closed and leads to the eliminations highlighted in yellow.

The Variants to the classical SK Loop also take in consideration

• 4 Pivots presenting the Givens signature
• the 16 Cells of the mini-Rows and mini-Columns associated with the Pivots

The further requirements for the Variants to the classical SK Loop are now the following:

1. the inner links and the outer links can use 1, 2 or 3 Candidates, as long as these 8 links use all the Candidates present in the 16 Cells of the mini-Rows and mini-Columns associated with the Pivots
2. the mini-Rows and mini-Columns associated with the Pivots can each contain 1 solution or 1 given, which are obviously excluded from the links

When these variant requirements are met, then the same eliminations as in the classical SK Loop can be made, i.e.

1. in the Row or Column containing two pivots, all Candidates of the outer link can be eliminated outside of the Squares containing the pivot
2. in a Square containing a pivot, all Candidates of the inner link outside the mini-Row and mini-Column

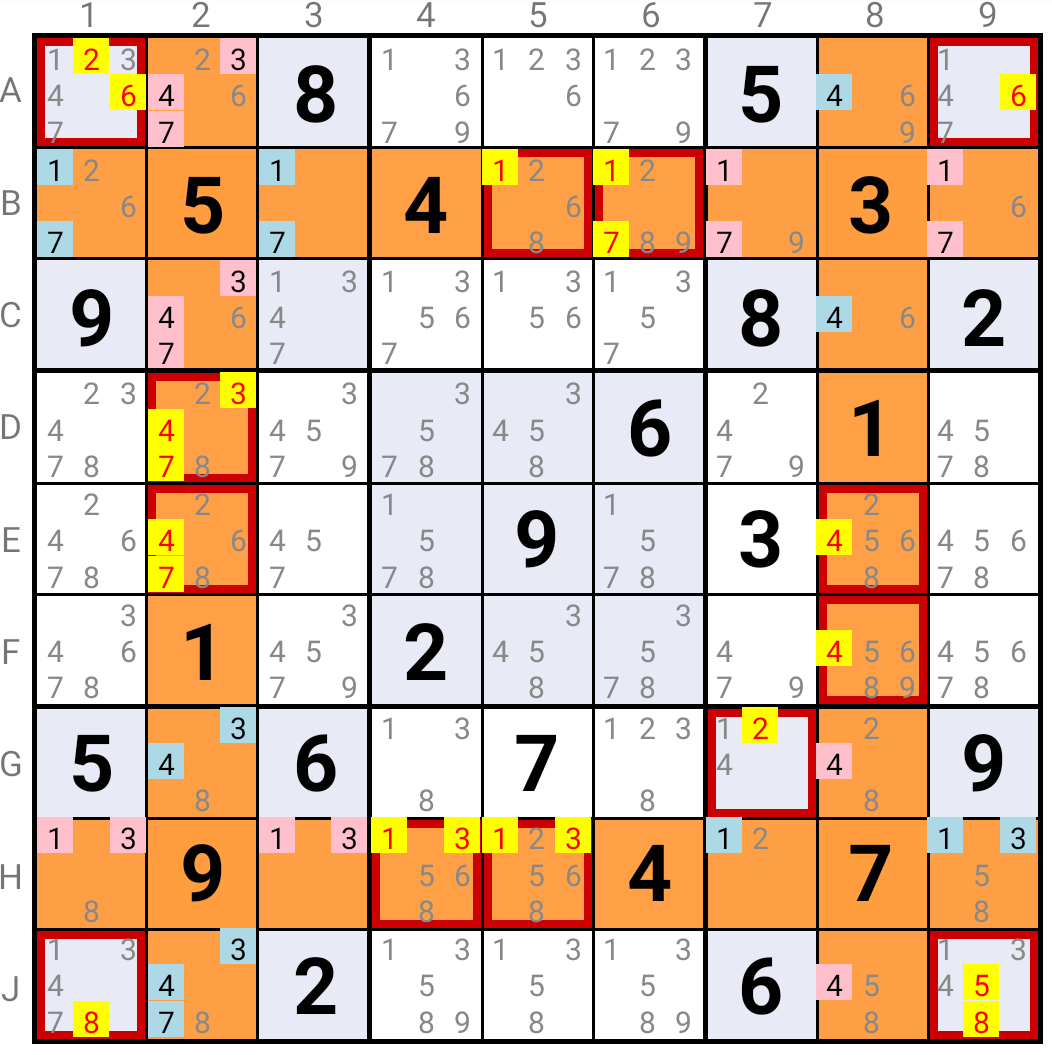
This first example shows a Variant SK Loop using single, double and triple links :

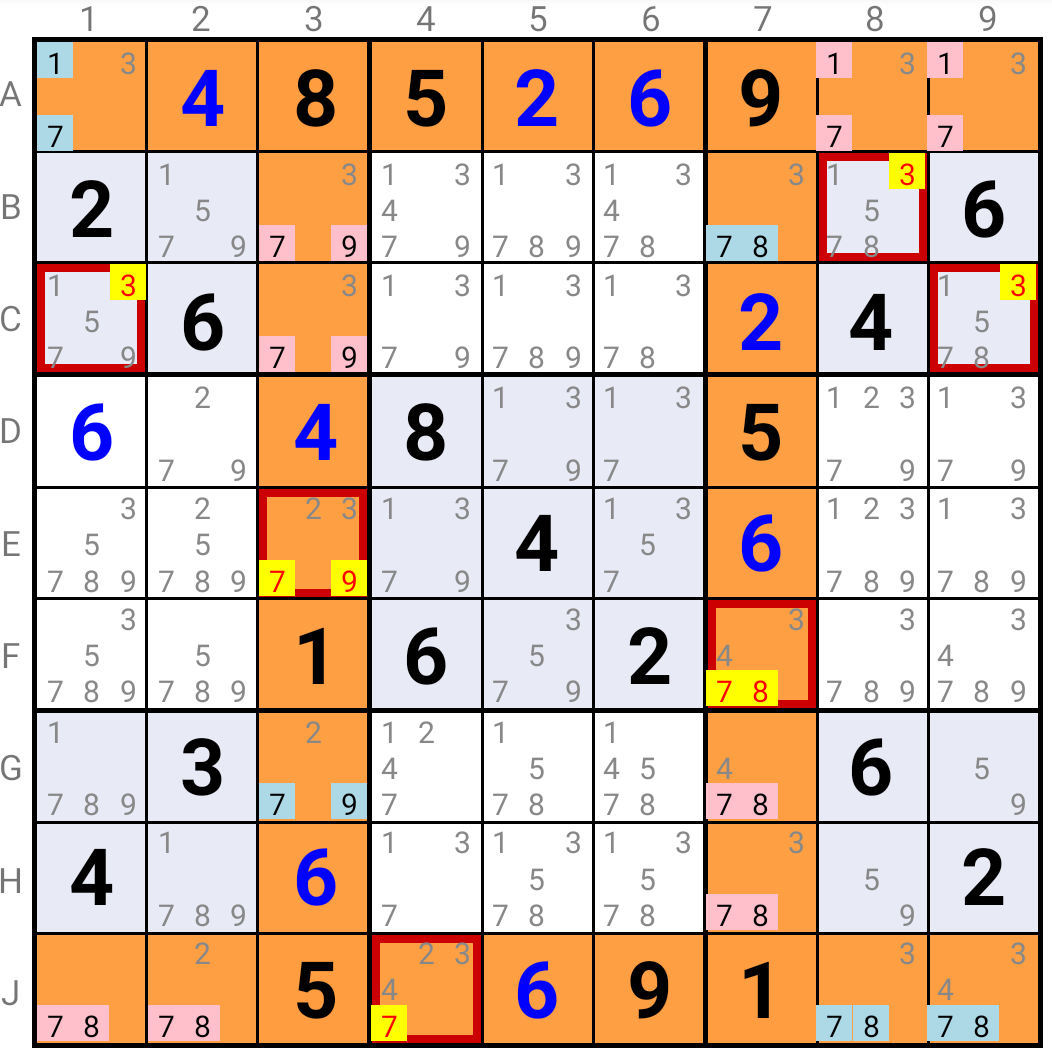
This second example shows a Variant SK Loop with solutions in the mini-Rows and mini-Columns associated with the Pivots :

You can practice this strategy by installing the SudokuCoach application on your Android™ device.