Exocet
Let us consider the following pattern:
| B B * | * . . | * . . |
| . . * | T1 M2 M2 | C2 . . |
| . . * | C1 . . | T2 M1 M1 |
| . . S | S . . | S . . |
| . . S | S . . | S . . |
| . . S | S . . | S . . |
| . . S | S . . | S . . |
| . . S | S . . | S . . |
| . . S | S . . | S . . |
or
| B B * | * . . | * . . |
| . . * | T1 . . | T2 . . |
| . . * | C1 M2 M2 | C2 M1 M1 |
| . . S | S . . | S . . |
| . . S | S . . | S . . |
| . . S | S . . | S . . |
| . . S | S . . | S . . |
| . . S | S . . | S . . |
| . . S | S . . | S . . |
where
- B identify the Base Cells
- T1 and T2 identify the Target Cells
- C1 and C2 identify the Companion Cells
- M1 and M2 identify the Mirror Cells
- CLb, CL1 and CL2 identify the Cross-Line Cells
- * identify the Escape Cells
and the following conditions:
- The Base Cells together contain 3 or 4 Candidates, that we call Base Candidates (outside these Cells and the Target Cells, they are called Base Digits)
- The Target Cells belong to the same Band as the Base Cells but do not see the Base Cells
- The Target Cells together contain at least the same 3 or 4 Candidates as the Base Cells
- C1 does not contain any Base Digit present in T1 and C2 does not contain any Base Digit present in T2
- The M1 Mirror Node contain the Base Digits present in T1 and the M2 Mirror Node contain those present in T2
- All instances of each Base Digit as a candidate or a given or a solved value in the S Cells must be confined to no more than two Cover Houses
If these conditions are met, then
- the Base Candidate that will be the solution in the first Base Cell will be the solution in one of the Target Cells and the Base Candidate that will be the solution in the other Base Cell will be the solution in the other Target Cell
- the Mirror Nodes must contain the same Base Digits as their associated Target Cells together with one digit that is false in the Base Cells
- the two Base Candidates that will be the solution in the Base Cells must each be true in two S Cells; one of which lying in the CLb Cross-Line
Such a pattern allows the following eliminations:
Rule 3 : any non-Base Candidate in a Target Cell is false
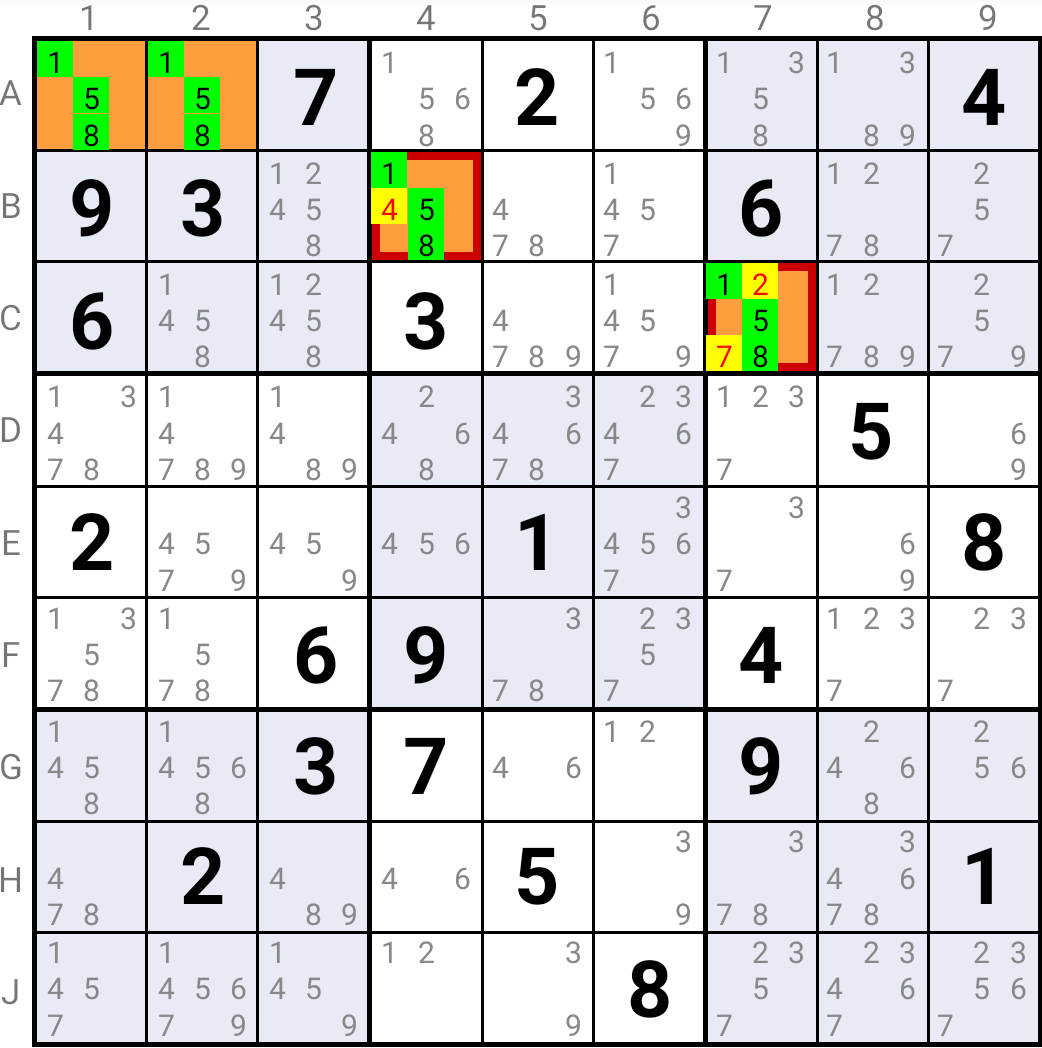
The solution in a Target Cell must be a Base Candidate.
Rule 4 : a Base Candidate that must be true in a Target Cell is false in the other Target Cell

The Target Cells must contain different Candidates.
Rule 5 : a Base Candidate that has a Cross-Line as an S Cell cover house must be false in the Target Cell in that Cross-Line
A Cross-Line is the entire Column (or Row when the Exocet pattern is column-oriented) containing the CLb, or CL1, or CL2 S Cells.
Let us consider a pattern with CL2 as cover house for a particular Base Candidate. To comply with the pattern requirements, this implies that this Candidate must be true in no more than one Cell in the CLb and CL1 S Cells.
If this Candidate were true in T2, then it would also be true in one of the Base Cells and thus also in CLb. This solution in CLb would eliminate the Candidate from CL1, forcing it as the solution in T1. However having the same Candidate as the solution in both T1 and T2 would invalidate the pattern.
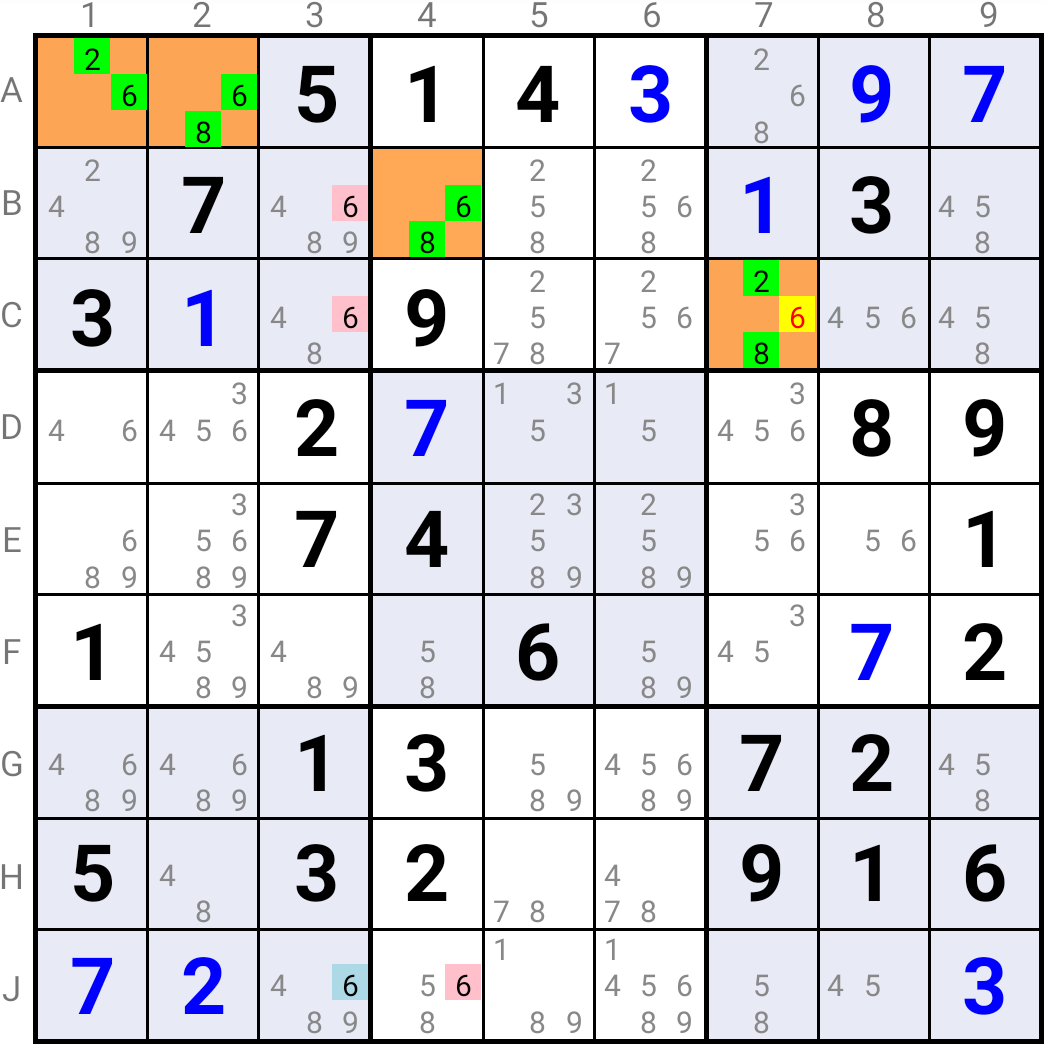
If Candidate 6 were true in C7, which is a Target Cell, this would imply it is a true Base Candidate. Being true in A1 or A2 would lead to it being true in J3 and B4. However B4 is a Target Cell and it must have a Base Candidate different from 6 as solution. Hence Candidate 6 can not be the solution in C7.
Rule 6 : any Base Candidate that can not be true in the Mirror Node associated with a Target Cell is false in that Target Cell.
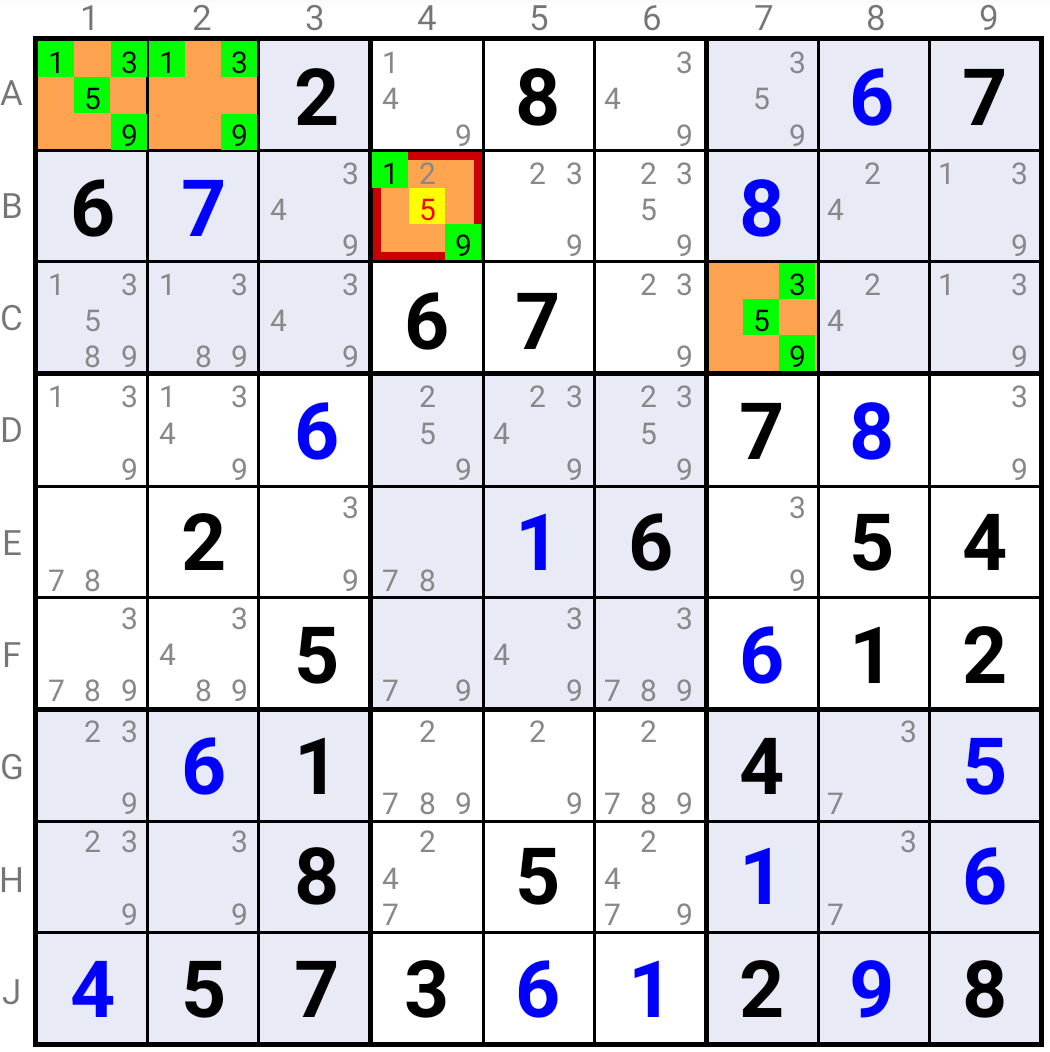
If such a Candidate is the solution in a Base Cell and a Target Cell, it must be the solution in the associated Mirror Node, because the Cells in this Mirror Node are the only possibilities left for this Candidate in the third Row of this Band.
Rule 7 : if a Cell in a Mirror Node does not contain any Base Candidates, then the other Cell in the same Mirror Node will be restricted to the Base Candidates present in the associated Target Cell
Indeed, the Base Candidate that is the solution in a Target Cell must be the solution in one of the Cells in its associated Mirror Node.
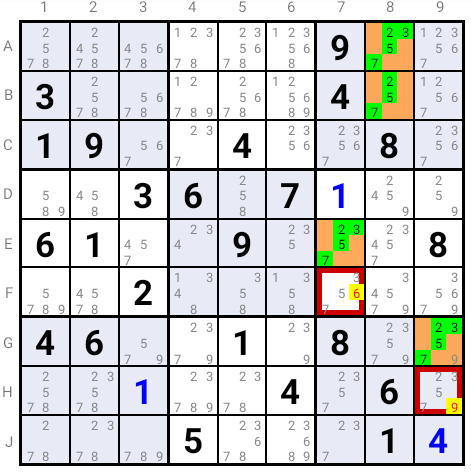
The Mirror Cells associated with the Target Cell in G9 are D7 and F7. One of them must contain one of the Base Digits 2, 3, 5 or 7.
As D7 is solved with a non-Base Digit, F7 must contain a Base Digit present in G9, which eliminates Candidate 6 in it.
Similarly, Candidate 9 can be eliminated in H9.
Rule 8 : if a Mirror Node contains only one possible non-Base Digit value, it is true in that Mirror Node and false in the cells in sight of it
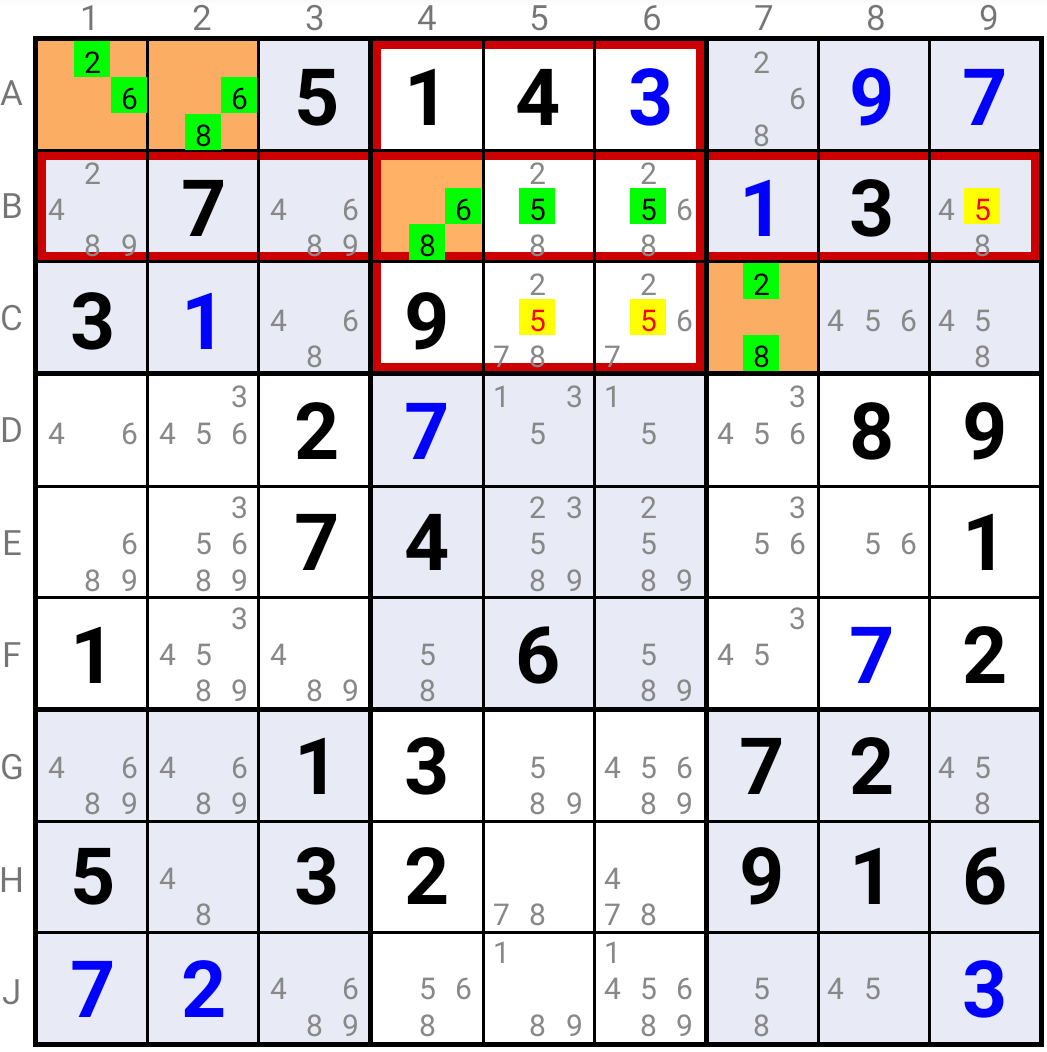
The two Cells in a Mirror Node must contain a Base Digit and a non-Base Digit, respectively.
Hence if there is only one possible non-Base Digit value in a Mirror Cell, it must be the solution in that Mirror Node and it can be eliminated in the Cells that see that Mirror Node.
Rule 9 : if a Mirror Node contains a locked digit, any other digits it contains of the same type (base or non-base) are false
If a Mirror Node contains a locked digit, this locked digit must be the solution in one of the Cells of the Mirror Node.
Because the two Cells in a Mirror Node must contain a Base Digit and a non-Base Digit, respectively, if the locked digit is a Base Digit, then all other Base Digits can be eliminated in the Mirror Node. Conversely, if it is a non-Base Digit, then all other a non-Base Digits can be eliminated in the Mirror Node.
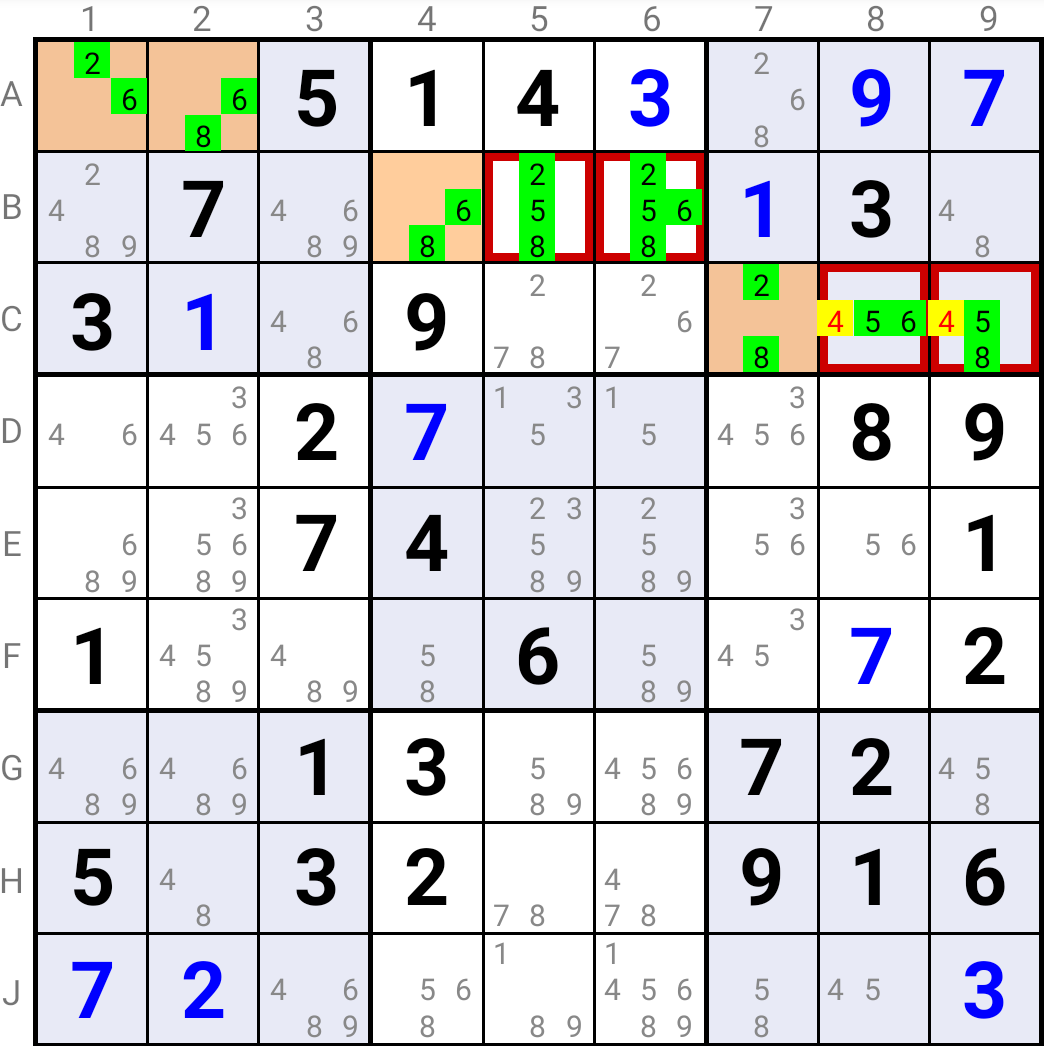
Being locked in C8 and C9, Candidate 5 must be the solution in one of these Cells. As these Cells are also the Mirror Cells for Target Cell B4, one of them must have Candidate 6 or Candidate 8 as its solution. Hence Candidate 4 can not be the solution in C8 or C9.
Rule 10 : a known Base Digit is false in all cells in full sight of either both Base Cells, or both Target Cells
A known Base Digit is a digit we know for sure is the solution in one of the Base Cells. If it is the solution in one of the Base Cells, then it must also be the solution in one of the Target Cells. Hence it can be eliminated in all cells that see both Base Cells or both Target Cells.
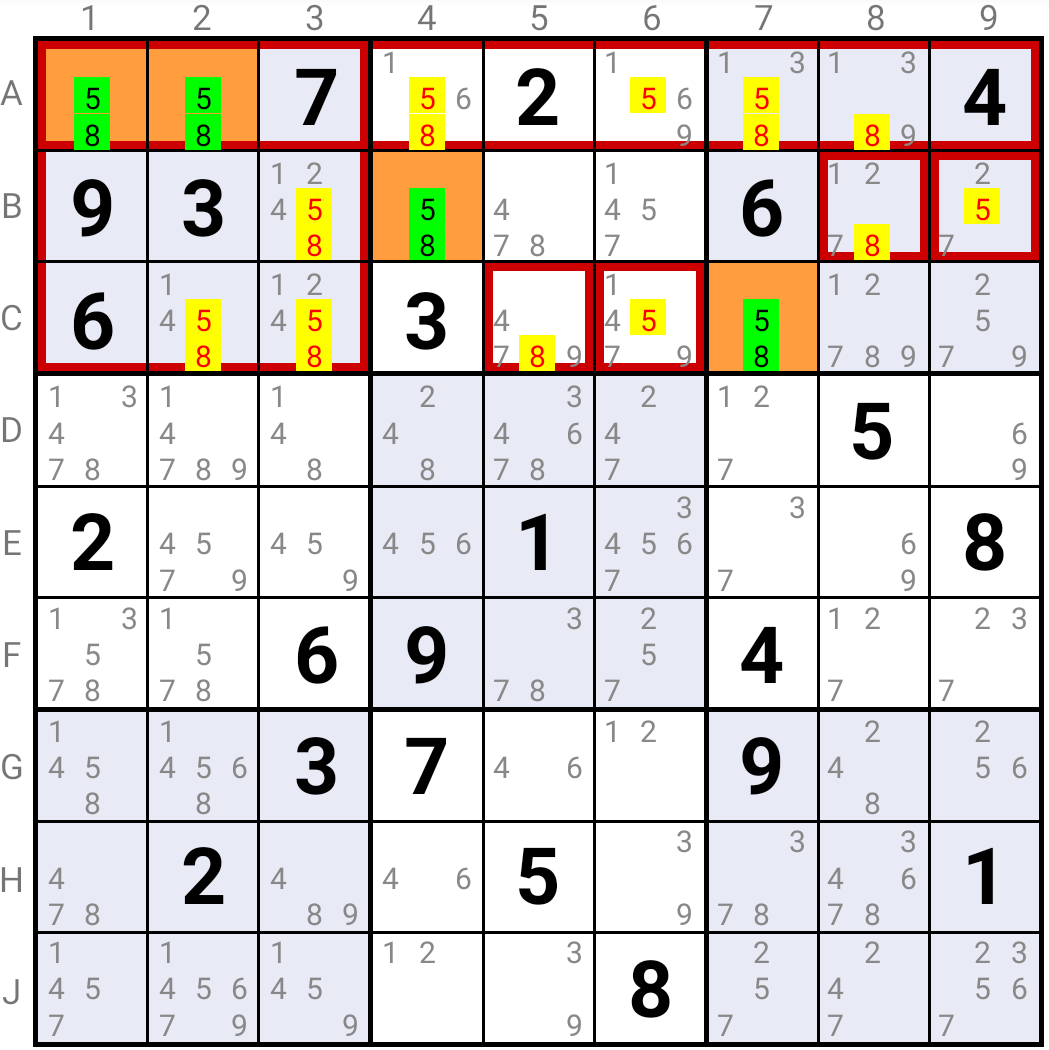
Candidate 5 must be the solution in either A1, or A2; hence it can be eliminated in all Cells that see both of these Cells.
It must also be the solution in either B4, or C7; hence it can be eliminated in all Cells that see both of these Cells.
Same reasoning for Candidate 8.
Rule 11 : a known Base Digit, or one that can only occur once in the Escape Cells, is false in the non-S cells in its Cover Houses
A known Base Digit, i.e. a digit we know for sure is the solution in one of the Base Cells, must be the solution in a Cell in the CLb S Cells and in a Cell of the S Cells associated with the Target Cell in which it is not the solution. Of course, these 2 Cells will belong to different Cover Houses.
However, the Exocet pattern requires that all instances of each Base Digit as a candidate or a given or a solved value in the S Cells be confined to no more than 2 Cover Houses.
Hence, a known Base Digit being true in one S Cells in each of the Cover Houses, it can be eliminated in all Cells of these Cover Houses except in the S Cells.
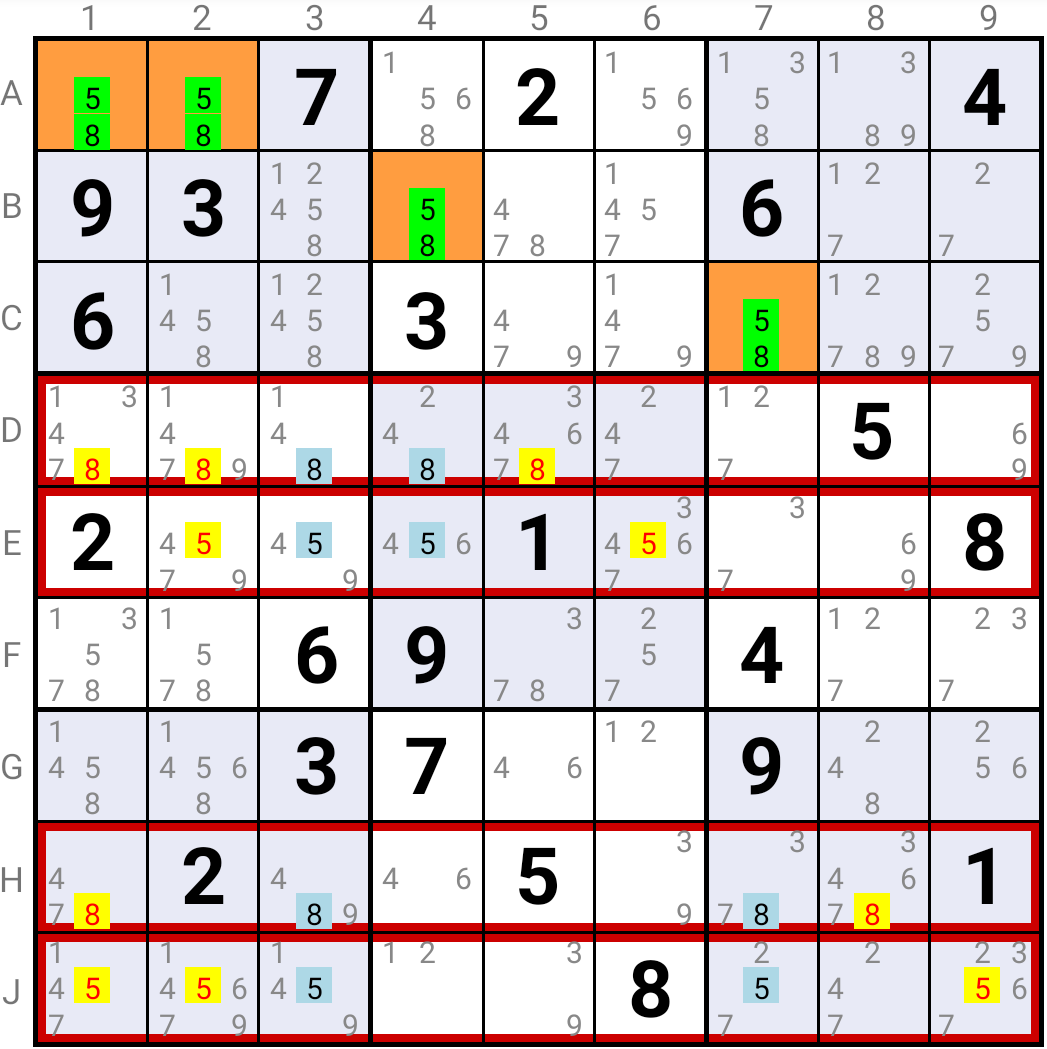
As Candidate 5 must be the solution in one of the Base Cells A1 or A2, it must be true in either E3 and J7, or in J3 and E5.
A similar reasoning holds for Candidate 8.
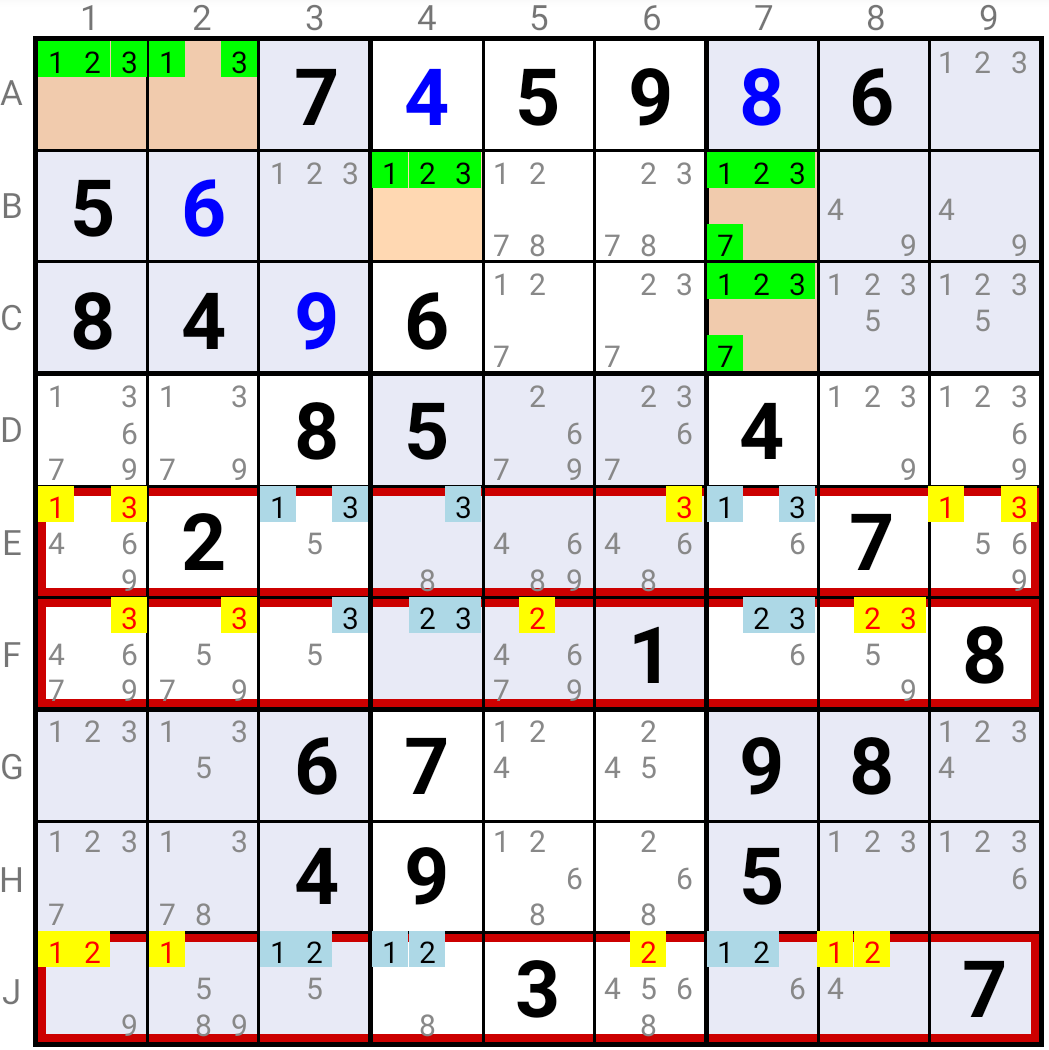
If Candidate 1 is not the solution in the Base Cells A1 or A2, then it can not be the solution in the Target cells B4 and B7/C7, either.
It must then be the solution in B3, J4 and E7. Which eliminates it in E1, E9, J1, J2 and J8.
A similar reasoning holds for Candidates 2 and 3.
Rule 12 : for a known Base Digit, any digit instance that would prevent 2 of its S Cells being true is false
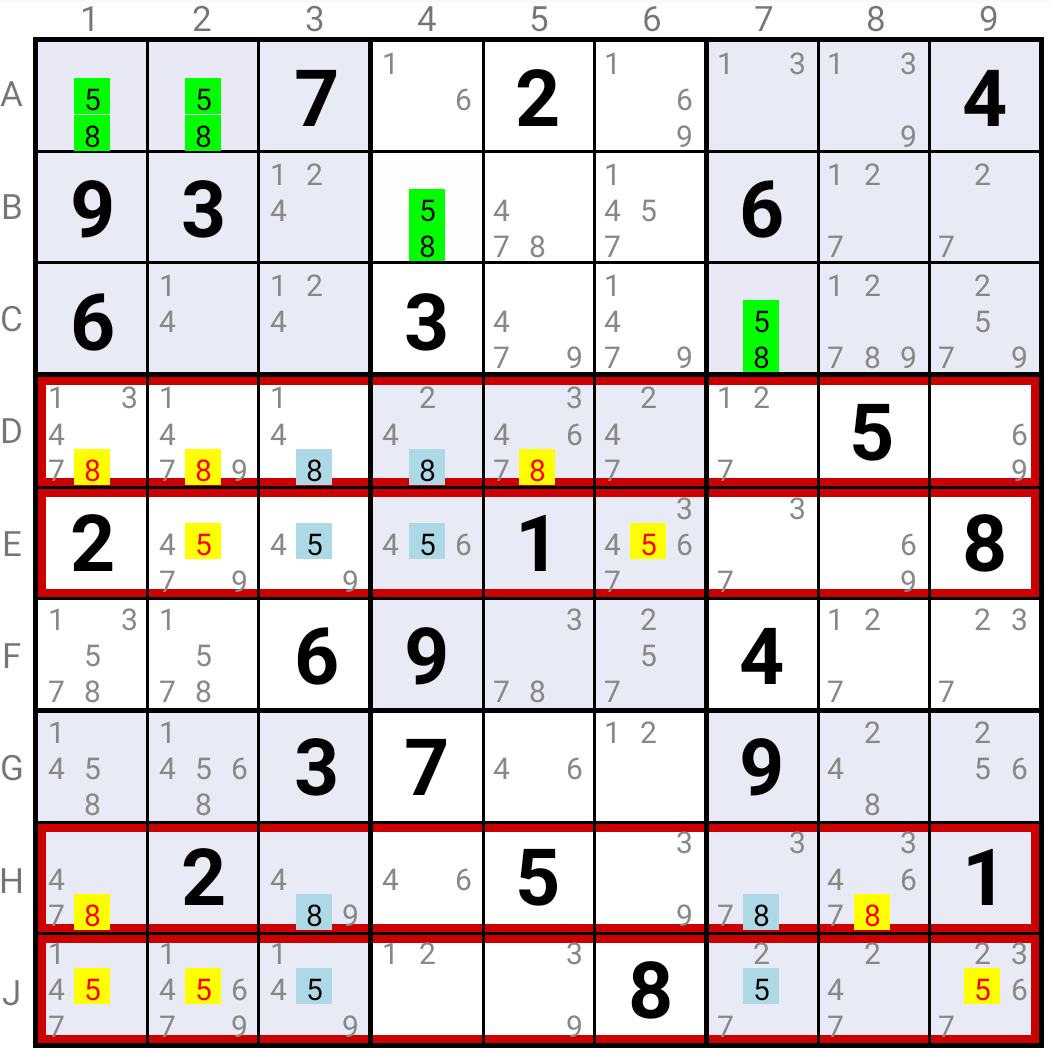
Incompatible Pairs : if all the combinations of a particular Base Candidate in one Base Cell with all the other Base Candidates in the other Base Cell would lead to the creation of Deadly Patterns, then this particular Base Candidate is false
In a well behaved Sudoku, Deadly Patterns, are forbidden.
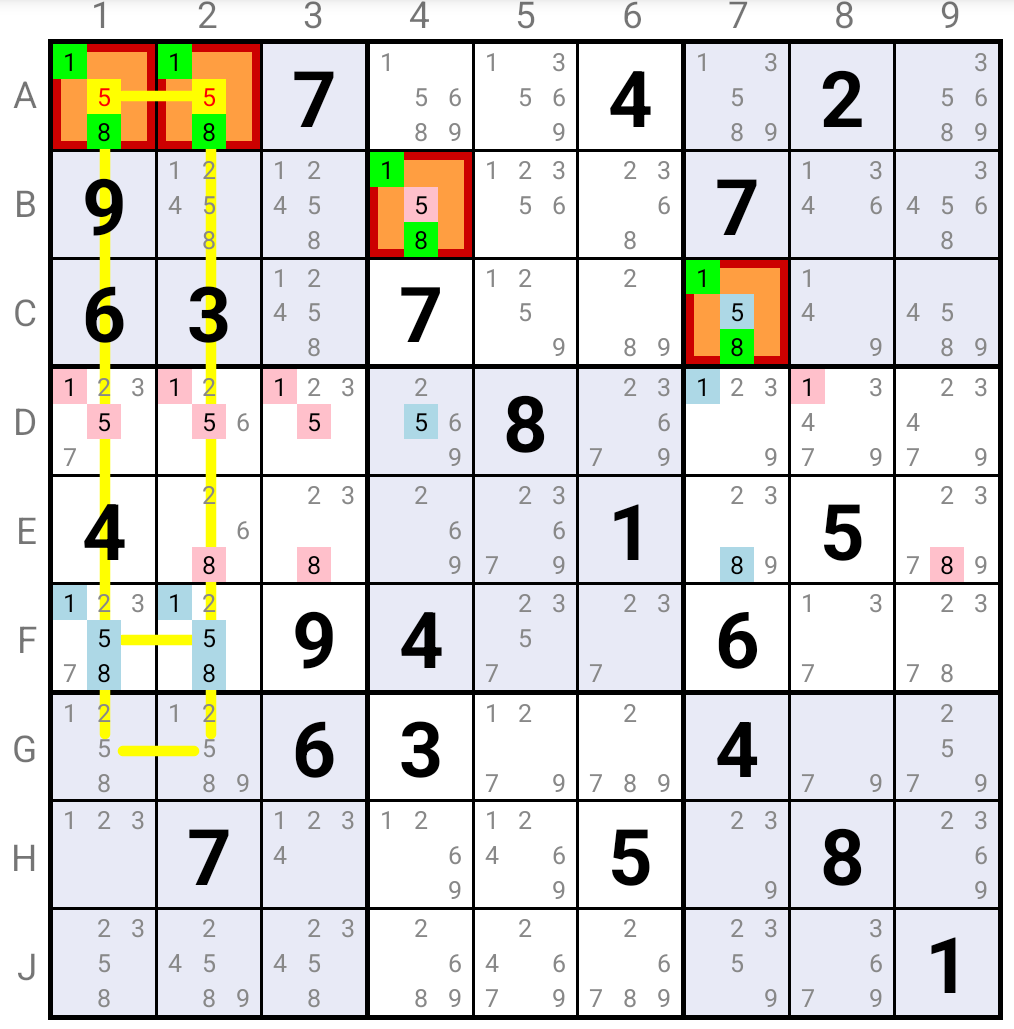
If Candidate 5 were the solution in A1 or A2, then it would have to be true in either B4, or C7.
In the latter case, it would then be false in B4, then true in D4, then false in D3, D2 and D1, and finally true in F1 or F2.
At the same time, either Candidate 1 or Candidate 8 would have to be false in C7.
If Candidate 1 were false in C7, it would have to be true in D7, then false in D3, D2 and D1, and finally true in F1 or F2.
If Candidate 8 were false in C7, it would have to be true in E7, then false in E3 and E2, and finally true in F1 or F2.
Hence, we would have a Deadly Pattern in A1/A2/F1/F2.
A similar reasoning considering Candidate 5 true in B4 woul lead to a Deadly Pattern in A1/A2/G1/G2.
Examples and rule numbering come from the JExocet Compendium.
You can practice this strategy by installing the SudokuCoach application on your Android™ device.
