Let us define an "Almost Locked Set" ("ALS" in short) as a set of n Cells in the same region (Row, Column or Square) containing in total exactly (n+1) Candidates: eg a "Bi-Value" Cell or two "Bi-Value" Cells with a common Candidate.

Let us define a "Locked Set" as a set of n Cells containing in total exactly n Candidates. The Cells must not necessarily belong to the same region, but each of these n Candidates must "see" (a Candidate "sees" another Candidate if both Candidates belong to the same region) all other Cells in the set where it is present; eg a Naked Pair is a Locked Set.

In the Almost Locked Set strategy we try to identify two ALS that have two Candidates in common.

Almost Locked Set Type 1

All the Cells in the first ALS that contain the first common Candidate can "see" all the Cells in the second ALS that contain this first common Candidate, then the second common Candidate can not be the solution for any Cell outside the two ALS that can "see" all Cells in both ALS that contain the second common Candidate.

Indeed, because of the condition set on the first common Candidate the two ALS together form a Locked Set; having the second common Candidate as solution for a Cell outside this Locked Set that can see all Cells in this set containing this second common Candidate would eliminate the second common Candidate from the Locked Set, leaving it with only (n-1) Candidates for n Cells.

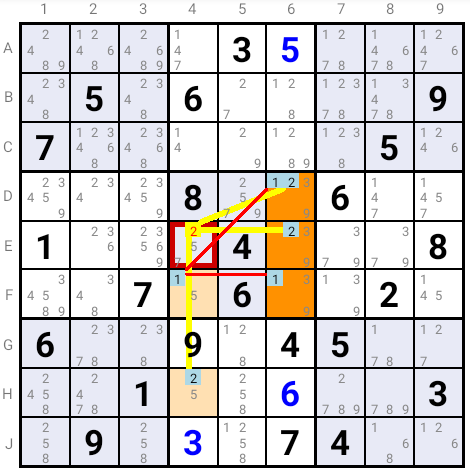
In this example 1 is the first common Candidate and 2 is the second common Candidate.
If Candidate 2 were the solution in E4, then Candidate 5 would be the solution in H4, Candidate 1 in F4, and the three Cells D6, E6 and F6 would have only two possible Candidates (3 and 9) which is not possible. Hence Candidate 2 can not be the solution in E4 and it can be eliminated in that cell.

Almost Locked Set Type 2

If all occurences of the first common candidate in each ALS can "see" all its occurences in the other ALS and if the same is also true for the second common Candidate, then the first common Candidate must be the solution in one of the ALS and the second common Candidate must be the solution in the other ALS.

Indeed,

• if none were the solution in one of the ALS, then this ALS would only contain (n-1) possible Candidates for n Cells, which is not possible
• if both were the solution in one of the ALS, then the other ALS would only contain (n-1) possible Candidates for n Cells, which is again not possible

This leads to a first set of eliminations: as the common candidates must be the solution in the ALS, they can be eliminated from all Cells that "see" all their occurences in the ALS.

As the first common Candidate is a solution in one ALS, it eliminates all its occurences in the other ALS, transforming this other ALS into a Locked Set. As the second common Candidate is a solution in this other ALS, it eliminates all its occurences in the first ALS, also transforming it into a Locked Set. This implies that the non-common Candidates must be the solutions inside their respective ALS, which in turn eliminates them from the Cells outside of the ALS that "see" them.

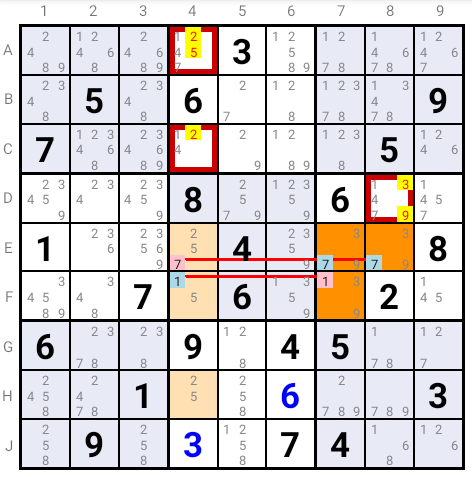
The Common Candidates are 1 and 7. The former must be the solution in one of the ALS and the latter in the second.

You can practice this strategy by installing the SudokuCoach application on your Android™ device.