Let us define an "Almost Locked Set" ("ALS" in short) as a set of n Cells in the same region (Row, Column or Square) containing in total exactly (n+1) Candidates: eg a "Bi-Value" Cell or two "Bi-Value" Cells with a common Candidate.

Let us define a "Locked Set" as a set of n Cells containing in total exactly n Candidates. The Cells must not necessarily belong to the same region, but each of these n Candidates must see all other Cells in the set where it is present; eg a Naked Pair is a Locked Set.

In this strategy, we are looking for a Cell that can see as many "ALS" as there are Candidates in the Cell. The reported discoverer of this strategy called this Cell the "stem" and the "ALS" the "petals", hence its name.

If each Candidate in the "stem" can see all the Cells of the selected "ALS" that contain the same Candidate, then a Candidate present in the "ALS" can not be the solution for any Cell outside the "ALS" that sees all the Cells in these "ALS" that contain this Candidate.

Indeed, the solution for the "stem" will reduce the related "ALS" to a "Locked Set". If the solution for a Cell outside this "ALS" eliminated a Candidate in this "Locked Set", then this set of n Cells would only have (n-1) possible Candidates.

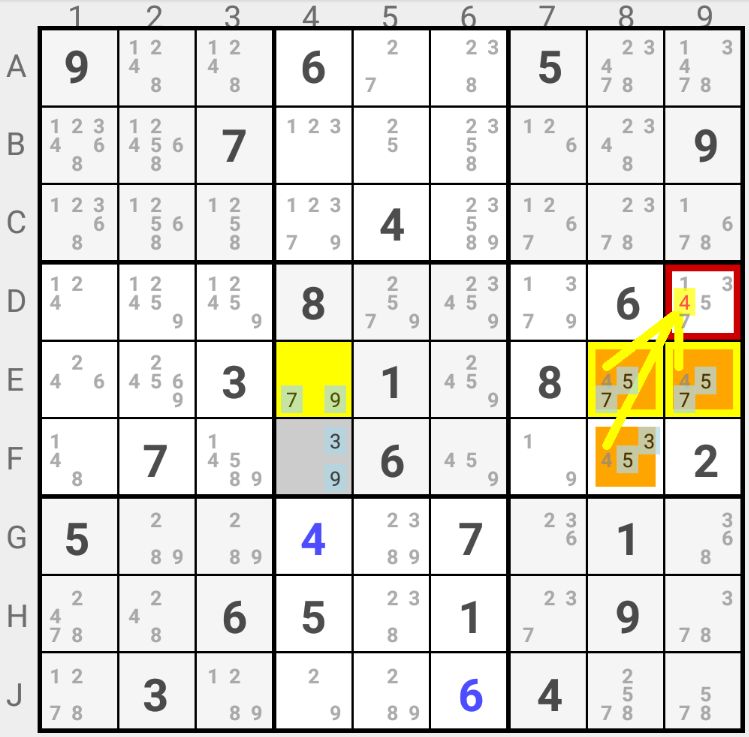
In this example F4 is the stem. Let's see how it propagates death to the petals.
If Candidate 9 is the solution in F4, then Candidate 7 is the solution in E4 and Candidate 3 in F8. Cells E8 and E9 form a Naked Pair based on Candidates 4 and 5 which eliminates Candidates 4 and 5 in D9.
If Candidate 3 is the solution in F4, then Candidate 9 is the solution in E4. Cells E8, E9 and F8 form a Naked Triple based on Candidates 4, 5 and 7 which eliminates Candidates 4, 5 and 7 in D9, and Candidate 7 in D7.

Another way to look at it consists in assuming that Candidate 4 is the solution in D9. Then the ALS made of E4, E8 and E9 becomes a Naked Triple based on Candidates 5, 7 and 9. This implies that Candidate 9 is the solution in E4, Candidate 3 in F4 which eliminates Candidate 3 in F8. But Cells E8 and E9 now form a Naked Pair based on Candidates 5 and 7 which eliminates Candidate 5 in F8 ... leaving F8 without any possible Candidate left. The assumption that Candidate 4 is the solution in D9 is wrong and Candidate 4 can be eliminated in D9.

You can practice this strategy by installing the SudokuCoach application on your Android™ device.