In the Digit Forcing Chain strategy we build two chains alternating Strong Link (also see note at the bottom of this page) and Weak Links starting from a single candidate in a particular Cell. The first chain starts with the candidate "OFF" and the second chain with the candidate "ON".

FORCING DIGIT Type 1 (always "ON") : the two chains meet in a Cell with the same candidate "ON". This candidate must be the solution for that Cell, as it is always "ON" whichever the initial state of the candidate in the starting Cell of the chain.

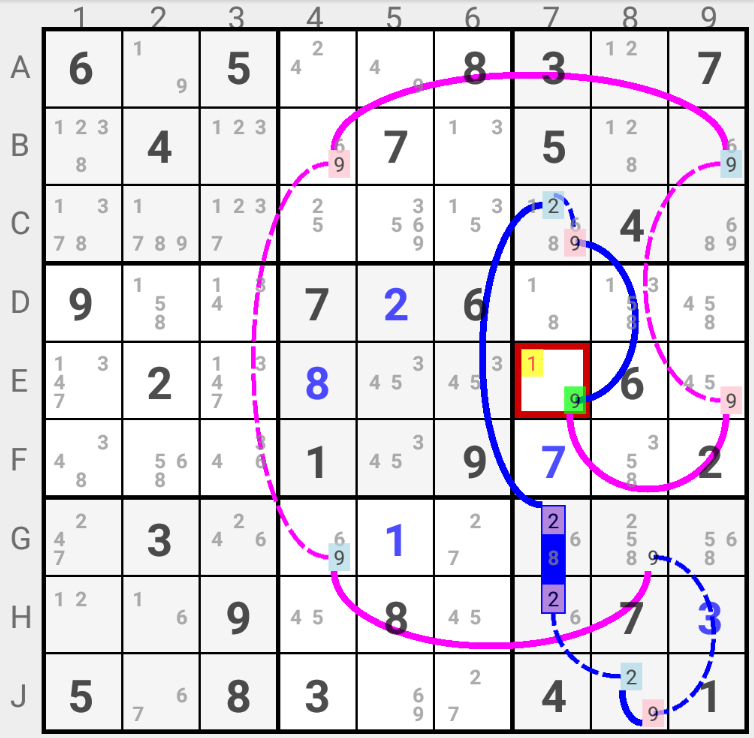
In this example if candidate 9 is "ON" in G8 then the blue Chain leads to candidate 9 being "ON" in E7.
If candidate 9 is "OFF" in G8 and if we follow the pink Chain, we eventually get to E7 with again candidate 9 "ON" in that Cell.
In all hypotheses (candidate 9 being or not being the solution in G8), candidate 9 is the solution in E7.

FORCING DIGIT Type 2 (always "OFF") : the two chains meet in a Cell with the same candidate "OFF". This candidate can not be the solution for that Cell, as it is always "OFF" whichever the initial state of the candidate in the starting Cell of the chain.

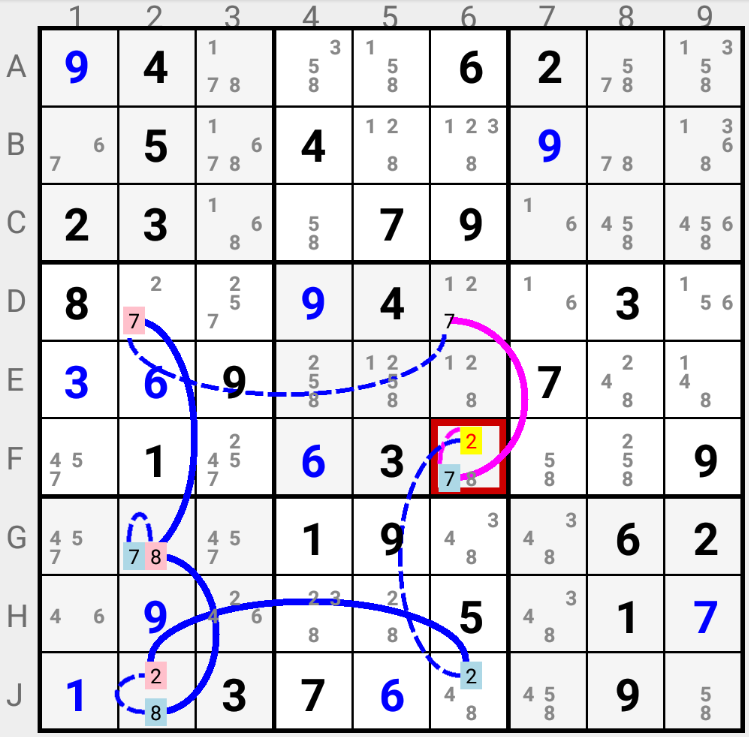
In this example, if candidate 7 is the solution in D6 (i.e. is "ON" in D6), then following the blue Chain candidate 2 is set "OFF" in F6.
If candidate 7 is not the solution in D6 (i.e. is "OFF" in D6), then following the pink Chain candidate 2 is again set "OFF" in F6.
In all hypotheses (candidate 7 being or not being the solution in D6), candidate 2 can not the solution in F6.

FORCING DIGIT Type 3 (two candidates "ON" in a Cell) : the two chains meet in a Cell with two different candidates "ON". As one of the chains identifies the solution for all its Nodes and as there are only two possible chains, the two candidates "ON" in the ending Cell are the only possible solutions for that Cell. Hence the other candidates in that Cell can not be the solution.

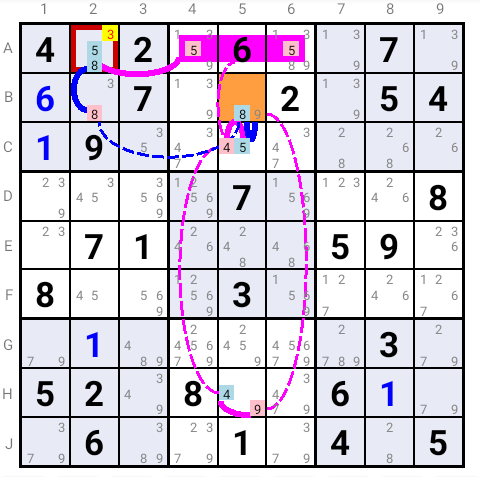
Here, if candidate 9 is the solution in B5, then candidate 5 is "ON" in A2; candidate 9 is not the solution in B5, then candidate 8 is "ON" in A2. Hence candidate 3 can not be the solution in A2.

FORCING DIGIT Type 4 (two candidates "ON" in a region) : the two chains set the same candidate twice "ON" in the same region (Row, Column or Square). As one of the chains identifies the solution for all its Nodes and as there are only two possible chains, the candidate can not be the solution in any other Cell of that region.

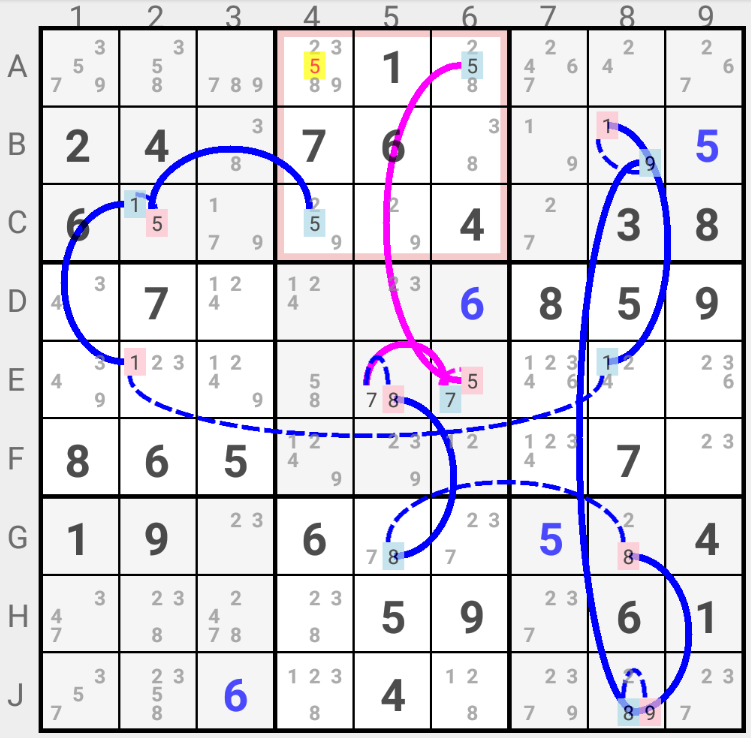
In this example, if candidate 7 is the solution in E5 (i.e. is "ON" in E5), then following the blue Chain candidate 5 is set "ON" in C4.
If candidate 7 is not the solution in E5 (i.e. is "OFF" in E5), then following the pink Chain candidate 5 is set "ON" in A6.
In all hypotheses (candidate 7 being or not being the solution in E5), candidate 5 must be the solution either in C4, or in A6. This implies that candidate 5 can not be the solution in any cell that sees C4 and A6, in this case Square "2", eliminating candidate 5 in A4.

NB: more formally, a Strong Link is the relationship that exists between two Cells in a region (Row, Column or Square) when these two Cells are the only Cells in that region that contain a particular candidate: if the candidate is not the solution for the first Cell, then it must be the solution for the second Cell, and vice-versa.
However, in the Chaining Strategies, we consider Strong Links as links going from a Cell or a group of Cells where we assert the candidate is not the solution (we say the candidate is in the "OFF" state) to a Cell or a group of Cells where it then must be the solution (we say the candidate is in the "ON" state).
If we consider a Bi-Value Cell, asserting that one of its candidates is not the solution implies that the other candidate must be the solution. Hence there also exists a Strong Link between the two candidates of a "Bi-Value" Cell.

A Weak Link as a link going from a Cell/group of Cells where the candidate is "ON" to a Cell/group of Cells where it is "OFF".

You can practice this strategy by installing the SudokuCoach application on your Android™ device.