Sue De Coq Extended (Type 1)

The basic Sue De Coq strategy uses two Bi-Value Cells and Cells at the intersection between the Square and the Row/Column containing these Bi-Value Cells.

The Type 1 extension replaces one or both Bi-Value Cells by multi-cell Almost Locked Sets ("ALS" in short). Each ALS must have two Candidates in common with the intersection cells. Whatever the solution for the ALS, it must contain one of these Candidates. Hence this Candidate can not be the solution in any of the intersection Cells. This being true for each ALS, there remains only two possible Candidates in the two intersection Cells or three possible Candidates in the three intersection Cells, justifying the eliminations outside of the Sue De Coq pattern.

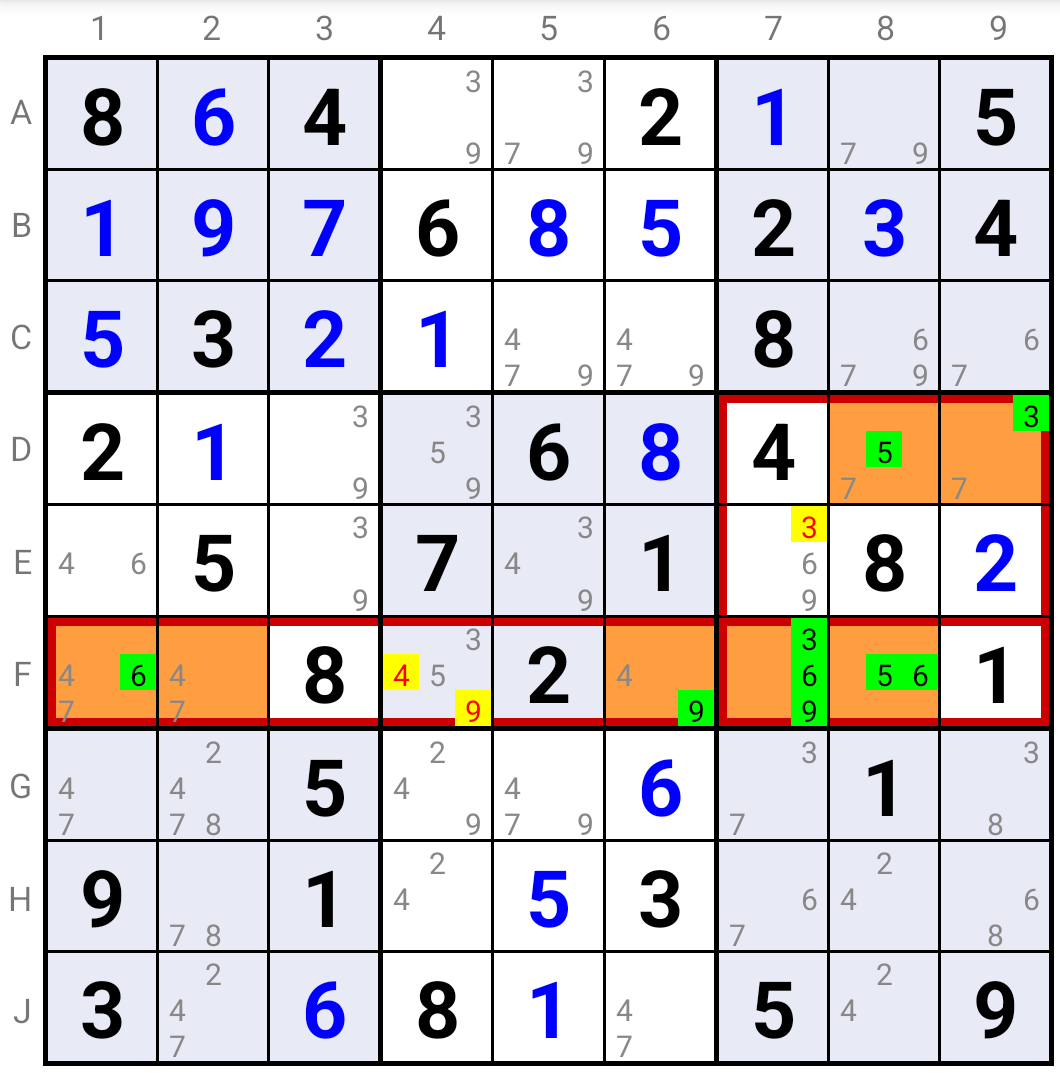
In the example above the Sue De Coq Extended Type 1 is based on ALS-1 in Cells D8 and D9, ALS-2 in Cells F1, F2 and F6; the intersection Cells are F7 and F8, and the two pairs of Candidates are (3, 5) and (6, 9).
ALS-1 must have Candidate 7 as solution in one of its Cells because Candidate 7 is not allowed in any other Cell of Square "6". The other Candidate in the Cell where it is the solution must be the solution in either F7, or F8.
Hence Candidate 6 or Candidate 9 must be the solution in the other intersection Cell, transforming ALS-2 into a Naked Triple. Leading to the indicated eliminations.

Sue De Coq Extended (Type 2)

In the basic Sue De Coq strategies and the above Sue De Coq Extended (Type 1) strategy each ALS (remember a Bi-Value is also an ALS) has two Candidates in common with the intersection Cells.

In the Sue De Coq Extended (Type 2) strategy, each ALS can have more than two Candidates in common with the intersection Cells. Let n1 be the number of Candidates that the first ALS has in common with the intersection Cells and n2 the number of Candidates that the second ALS has in common with the intersection Cells. If the considered intersection Cells contain these n1 + n2 Candidates, then the Sue De Coq elimination rules apply.

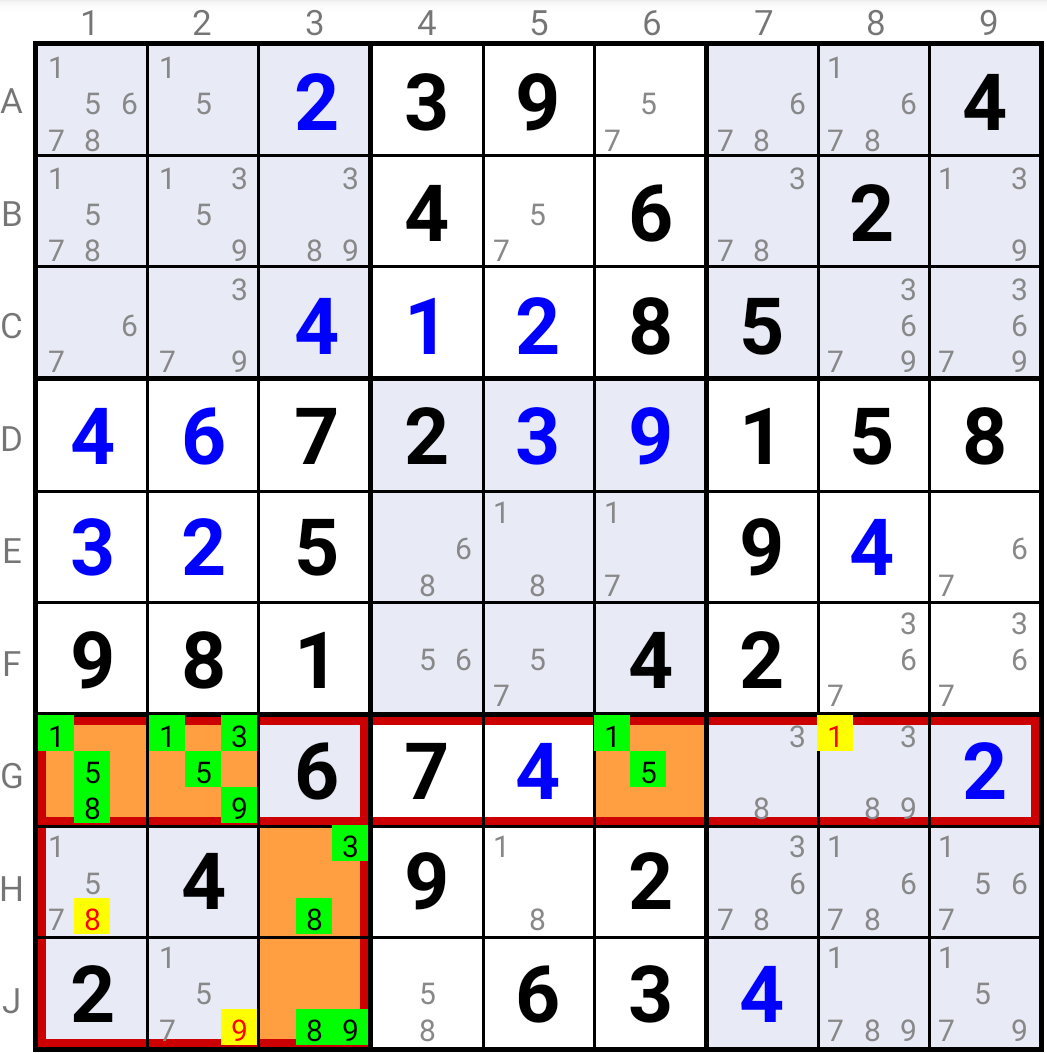
In the example above the Sue De Coq Extended Type 2 is based on ALS-1 in Cells H3 and J3, ALS-2 in Cell G6; the intersection Cells are G1 and G2, and the two groups of Candidates are (3, 8, 9) and (1, 5).
Whatever the solution in ALS-2, the combined Cells of ALS-1 and the intersection Cells become a Naked Quad.

You can practice this strategy by installing the SudokuCoach application on your Android™ device.