Sue De Coq
Sue de Coq Type 1
If it is possible to find two Bi-Value Cells that
- have no common Candidate
- with the first Cell in a Square (Square-1) and the second one in a Row (Row-2) that has Cells in common with Square-1
- but are not on the same Row.
If two Cells among the Cells that are common to Square-1 and Row-2 only contain combinations of the Candidates present in the two Bi-Value Cells, then these four Cells form a pattern called Sue De Coq Type 1.
Such a pattern allows the elimination of
- all Candidates present in the first Bi-Value Cell from Square-1
- all Candidates present in the second Bi-Value Cell from Row-2
Indeed, the four Cells in the pattern contain only combinations of four Candidates that see each others. Each of these Candidates must be the solution in one of the Cells of the pattern.
The reasoning is also applicable when you replace "Row" by "Column".

In the example above the Sue De Coq Type 1 is based on the Bi-Value Cells J7 and A8, and Cells H8 and J8. Because these Cells only contain combinations of Candidates 5, 6, 8 and 9, candidate 9 must be the solution in either J7, or J8, or H8, which eliminates it from H7 and H9; candidate 6 must be the solution in either A8, or H8, which eliminates it from E8. Similarly, candidate 8 must be the solution in either A8, or H8, or J8, which eliminates it from E8.
Sue de Coq Type 2
If it is possible to find two Bi-Value Cells that
- have no common Candidate
- with the first Cell in a Square (Square-1) and the second one in a Row (Row-2) that has Cells in common with Square-1
- but are not on the same Row.
If the Cells that are common to Square-1 and Row-2 only contain combinations of the Candidates present in the two Bi-Value Cells plus one other Candidate, then these five Cells form a pattern called Sue De Coq Type 2.
Such a pattern allows the elimination of
- all Candidates present in the first Bi-Value Cell from Square-1
- all Candidates present in the second Bi-Value Cell from Row-2
- the other Candidate from both Square-1 and Row-2
Indeed, the five Cells in the pattern contain only combinations of five Candidates that see each others. Each of these Candidates must be the solution in one of the Cells of the pattern.
The reasoning is also applicable when you replace "Row" by "Column".
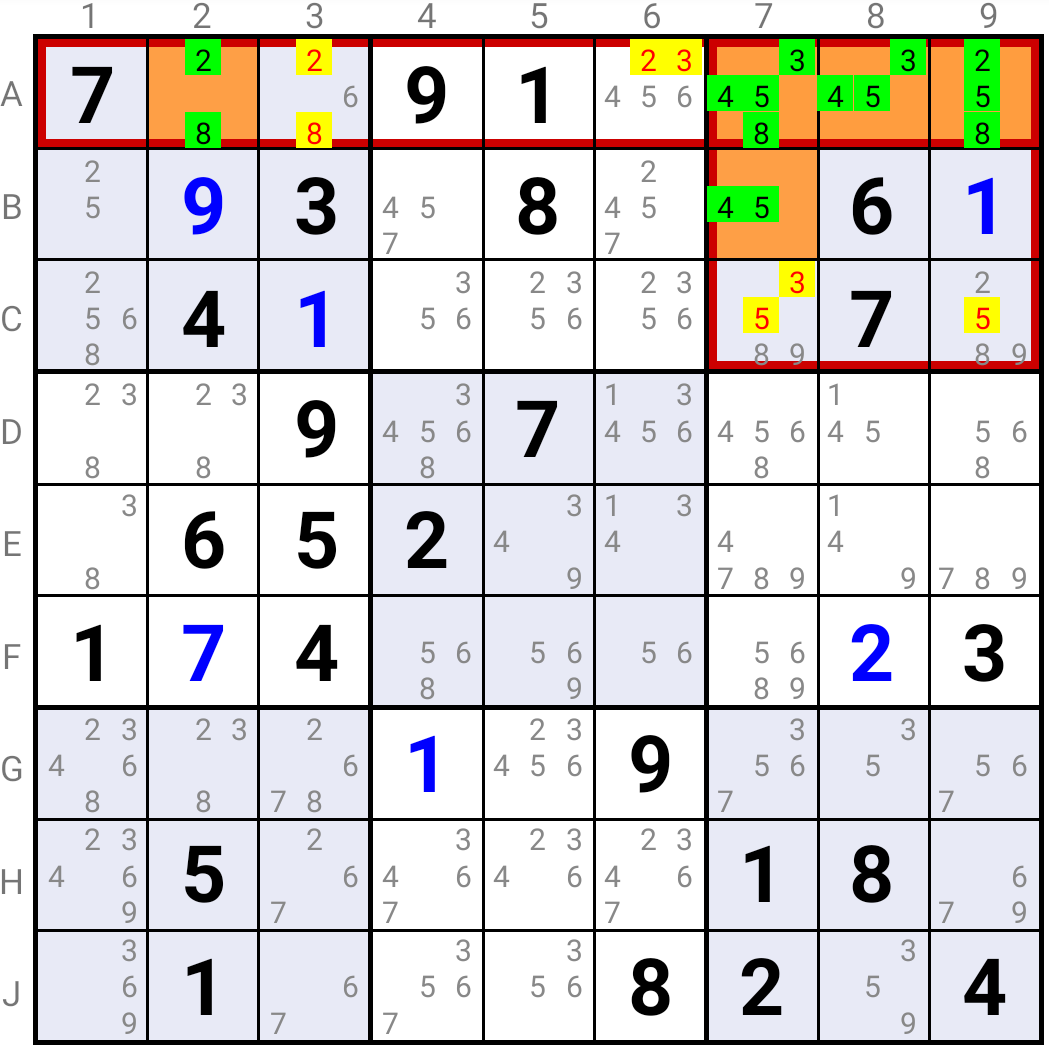
In the example above the Sue De Coq Type 2 is based on the Bi-Value Cells B7 and A2, and Cells A7, A8 and A9. Because these Cells only contain combinations of Candidates 2, 3, 4, 5 and 8, candidate 5 must be the solution in either B7, or A7, or A8, or A9, which eliminates it from C7 and C9; candidate 2 must be the solution in either A2, or A9, which eliminates it from A3 and A6. Similarly, candidate 8 must be the solution in either A2, or A7, or A9, which eliminates it from A3. Finally, candidate 3 must be the solution in either A7, or A8, or A9, which eliminates it from A6 and C7.
You can practice this strategy by installing the SudokuCoach application on your Android™ device.
