Consider two Strong Links for the same Candidate having a Cell in common. If the other node of each link consists in a single Cell and if the Candidate is false in these monoCell nodes, then it must be true in the common Cell. Hence the Candidate must be true in one of these three Cells.

Such a pattern has been called a Firework by the discoverer of this strategy. All examples come from this blog.

Triple Firework

If one can find a combination of three Fireworks that have the same common Cell and monoCell nodes, then one of their Candidates can not be true in the monoCell nodes (there are only two of them) and hence it must be true in the common Cell, which implies that the other two Candidates are true in their monoCell nodes.

Conclusion: three Candidates that must be true in three Cells implies that all the other Candidates in these Cells can be deleted.

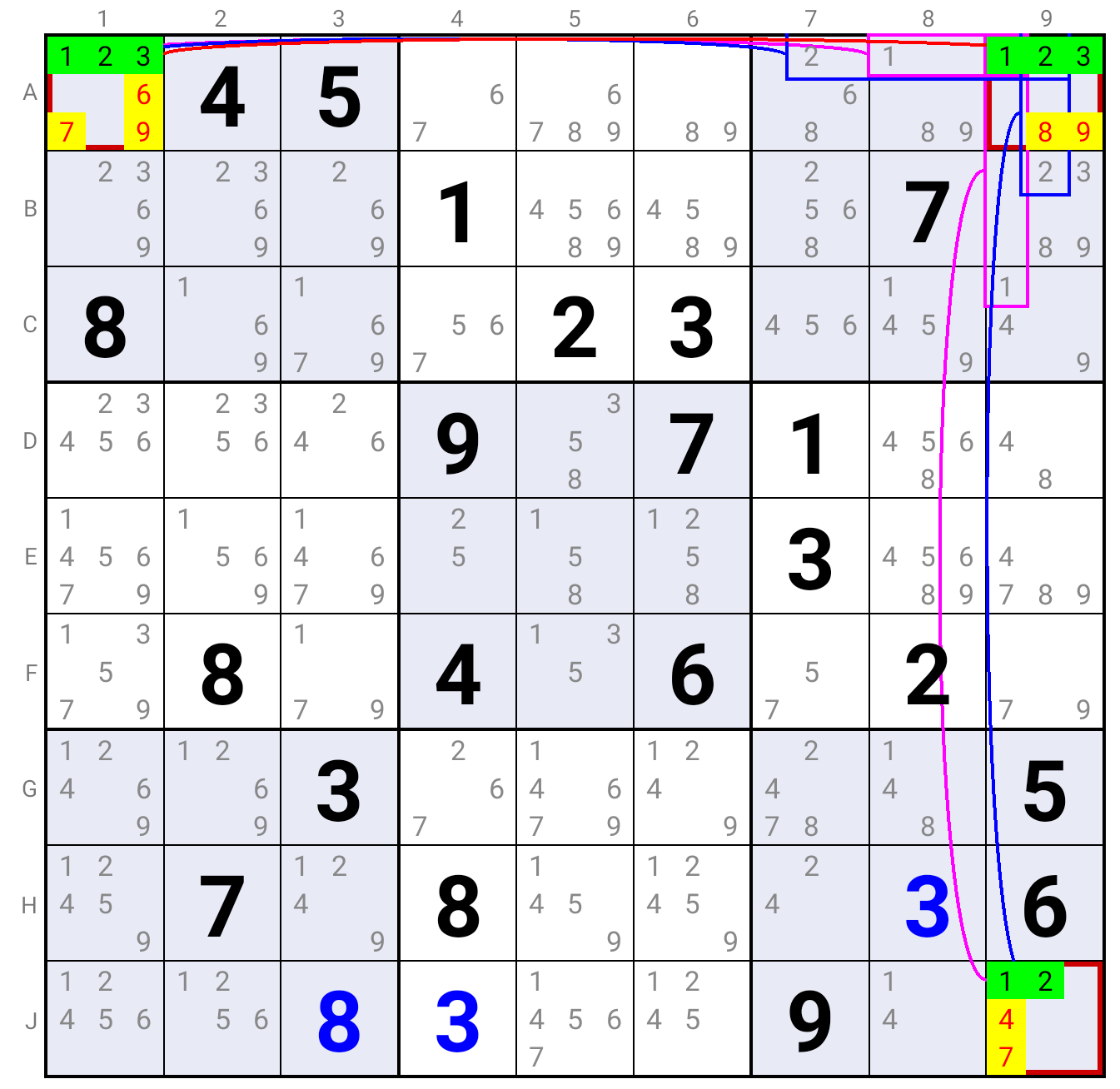
It is worth noting that one or two of these Fireworks can consist of Strong Links made of two single Cells as long as these Cells coincide with the common Cell and the monoCell nodes of the third Firework (which must be a true Firework).
This is the case in the example where we have two Fireworks based on Candidates 1 and 2, while the third Firework is a Strong Link for Candidate 3 on Cells A1 and A9.

Quadruple Firework

If one can find

• two Fireworks that have the same common Cell and monoCell nodes,
• two other Fireworks for two other Candidates that have the same monoCell nodes as the first two Fireworks and a common Cell that is different from the common Cell of the first two Fireworks

then these four Candidates must be true in the four Cells of the pattern and all the other Candidates in these Cells can be deleted.

Indeed, one Candidate of the first pair of Fireworks must be true in one of the monoCell nodes (they can not be simultaneously true in the common Cell).
This is also true for the second pair of Fireworks.
Which implies that the second Candidate of each Firework must be true in the common Cell of its Firework.

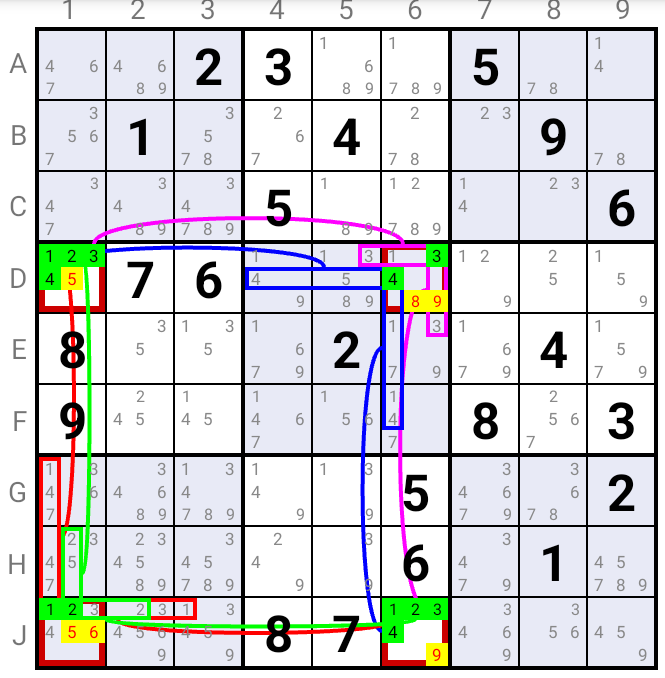
W-wing Firework

If one can find two Fireworks that have the same common Cell and monoCell nodes
and if these monoCell nodes each see a Bi-value Cell containing the same Candidates as these Fireworks
then any such Candidate that simultaneously sees the monoCell nodes and the Bi-value Cells can be deleted.

Indeed, a Candidate of a Firework must be true in one of the monoCell nodes or in the common Cell.
If it is true in the monoCell node, this eliminates it directly in the target Cell.
If it is true in the common Cell, then the second Candidate is true in one of the monoCell nodes, which eliminates it in the Bi-value Cell it sees. This in turn implies that the former Candidate is true in this Bi-value Cell, which eliminates it in the target Cell.

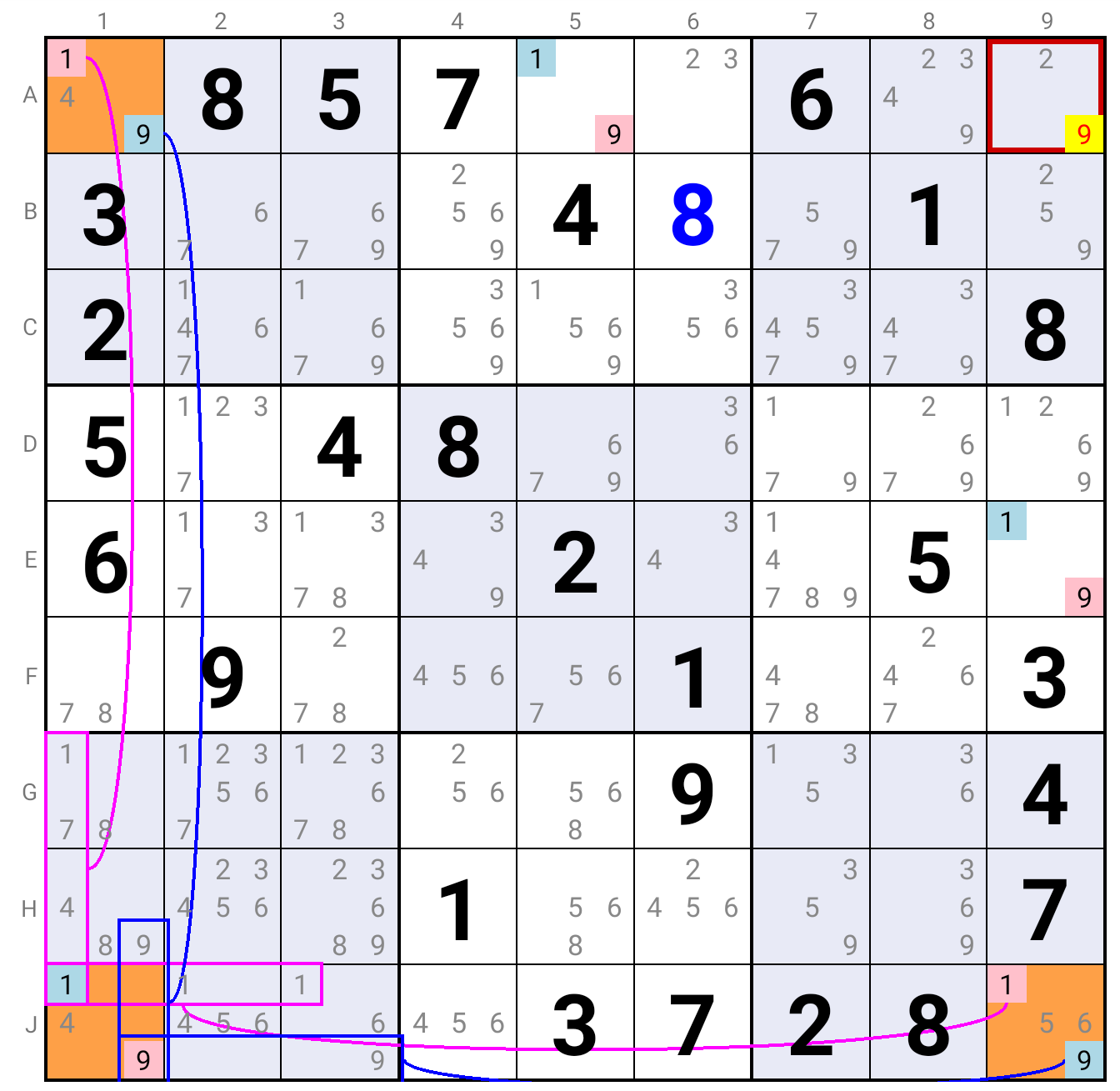
L-wing Firework

If one can find two Fireworks that have the same common Cell and monoCell nodes and if

• these monoCell nodes both contain another Candidate,
• this other Candidate is present in a Cell that sees the two monoCell nodes
• and is not present in any other Cell than the monoCell node in the same Row/Column (the monoCell node and that Cell form a Strong Link in that Row/Column)

then this Candidate can be deleted from the other monoCell node.

Indeed, being in a Strong Link, this Candidate is true either in the monoCell node, or in the Cell that sees the two monoCell nodes.
In the former case, the two Candidates of the Fireworks must be true in the common Cell and the same Row/Column as that monoCell node, whith the one not true in the common Cell mandatory true in the other monoCell node.
In the latter case, it eliminates it directly in the other monoCell node.
Hence the Candidate can never be true in the other monoCell node.

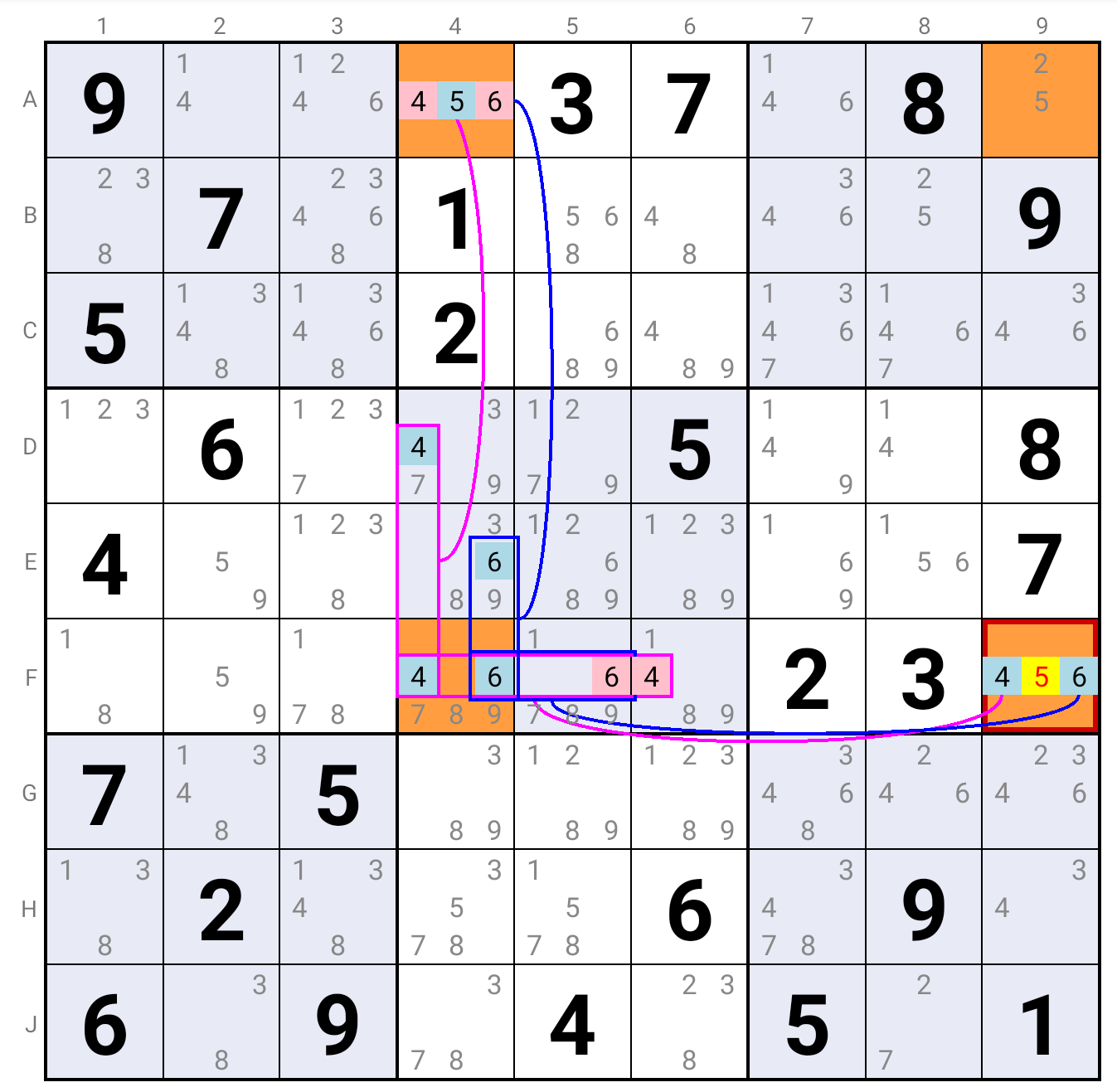
In this example, if Candidate 5 is true in A9, then 5 is eliminated in F9.
If it is true in A4, then Candidate 4 must be true in F4 or D4.

• In the former case, Candidate 6 must be true in E4, then false in F5 and true again in F9
• In the latter case, Candidate 4 must be false in F4 and in F6, then true in F9

ALS-wing Firework

If one can find two pairs of Fireworks with

• the Fireworks in each pair having the same common Cell and monoCell nodes,
• all four monoCell nodes seeing the same Bi-value Cell containing the same Candidates as these Fireworks

then two sets of eliminations are available:

• in the common Cell of each Firework : all Candidates different from the Candidates on which the Fireworks are based
• in the Row/Column containing the monoCell nodes and the Bi-value Cell : all Candidates on which the Fireworks are based, except in the monoCell nodes and in the Bi-value Cell, of course

Indeed, being seen by them, the Candidate that is true in the Bi-value Cell is eliminated from all four monoCell nodes, which implies that it is true in the common Cell of each Firework.
A Candidate on which a Firework is based that is not true in its common Cell must be true in one of its monoCell nodes.

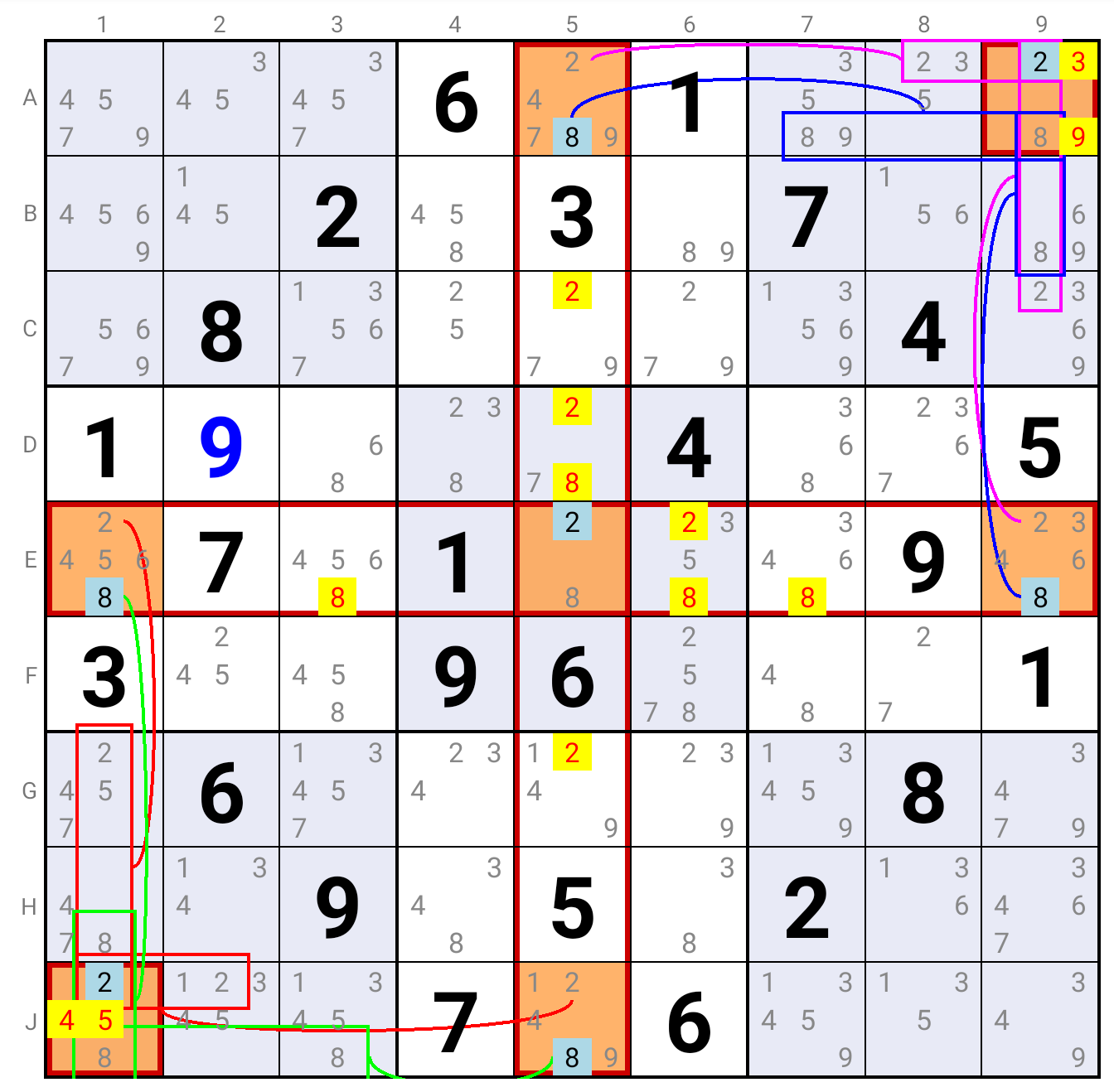
In the example, if Candidate 2 is true in the E5, then it is false in all four monoCell nodes (A5, E9, J5 and E1) and it must be true in the common Cell (A9 and J1) of each Firework.
This implies that Candidate 8 is true either in A5, or in E9. Which eliminates it from J5 or E1, respectively. Not being true in the common Cell J1 and in one of the monoCell nodes J5 or E1 implies it must be true in the other monoCell node (E1 or J5, respectively).
In any case, 8 must be true in A5 or in J5, and in E1 or E9. Hence the eliminations.

For the readability of the explanation, the hypothesis of Candidate 8 being true in A5 has not been illustrated. However the reasoning is identical.

NB: more formally, a Strong Link is the relationship that exists between two Cells in a region (Row, Column or Square) when these two Cells are the only Cells in that region that contain a particular candidate: if the candidate is not the solution for the first Cell, then it must be the solution for the second Cell, and vice-versa.
However, in the Chaining Strategies, we consider Strong Links as links going from a Cell or a group of Cells where we assert the candidate is not the solution (we say the candidate is in the "OFF" state) to a Cell or a group of Cells where it then must be the solution (we say the candidate is in the "ON" state).
If we consider a Bi-Value Cell, asserting that one of its candidates is not the solution implies that the other candidate must be the solution. Hence there also exists a Strong Link between the two candidates of a "Bi-Value" Cell.

A Weak Link as a link going from a Cell/group of Cells where the candidate is "ON" to a Cell/group of Cells where it is "OFF".

You can practice this strategy by installing the SudokuCoach application on your Android™ device.