If two Strong Links (also see note at the bottom of this page) share a common Cell, we can form a Chain of three Cells with the common Cell in the middle. If we assume that the candidate in the Cell at one end of the Chain is not the solution for that Cell, then it must be the solution for the next Cell in the Chain because of the definition of a Strong Link. This, in turn and for the same reason, implies that the candidate can not be the solution for the third Cell in the Chain.

Conversely if we assume that the candidate in the Cell at one end of the Chain is the solution for that Cell, then it can not be the solution for the middle Cell and it must be the solution in the other end Cell of the Chain.

If we consider a longer Chain exclusively made of Strong Links, the successive Nodes alternate from one state to the other.

This strategy analyzes such chains and uses colors to display these states. Because there are only two possible states, all candidates with the same color simultaneously must be the solution or can not be the solution.

3D MEDUSA (SAME COLOR TWICE IN A CELL) : We know that one of the two colors is the solution. As two candidates can not simultaneously be the solution for a Cell, the corresponding color can not be the solution; all candidates with this color can be eliminated. The other color is the solution.

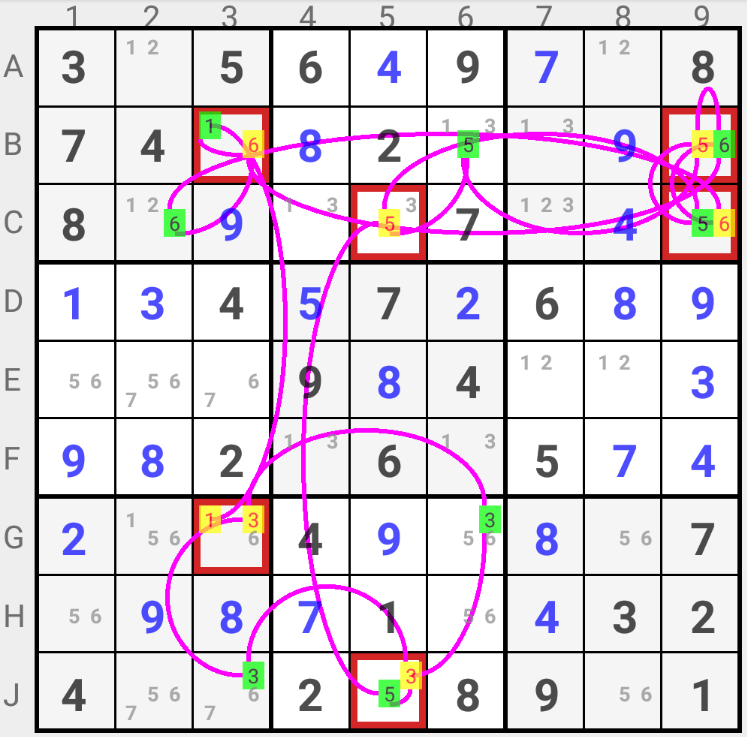
In the example, starting with coloring candidate 3 in J3 leads to candidates 1 and 3 in G3 being both colored in yellow. As two different candidates can not be the solution in a particular Cell, the yellow chain can not identify the solution. The candidates colored in green are the solution and all candidates colored in yellow can be eliminated.

3D MEDUSA (TWICE IN A UNIT) : if two Nodes in the Chain belong to the same region (Row, Column or Square) and if they have the same color for the same candidate, then this color can not be the solution because a candidate can not be the solution for two cells in the same region; all candidates with this color can be eliminated. Hence the other color is the solution.

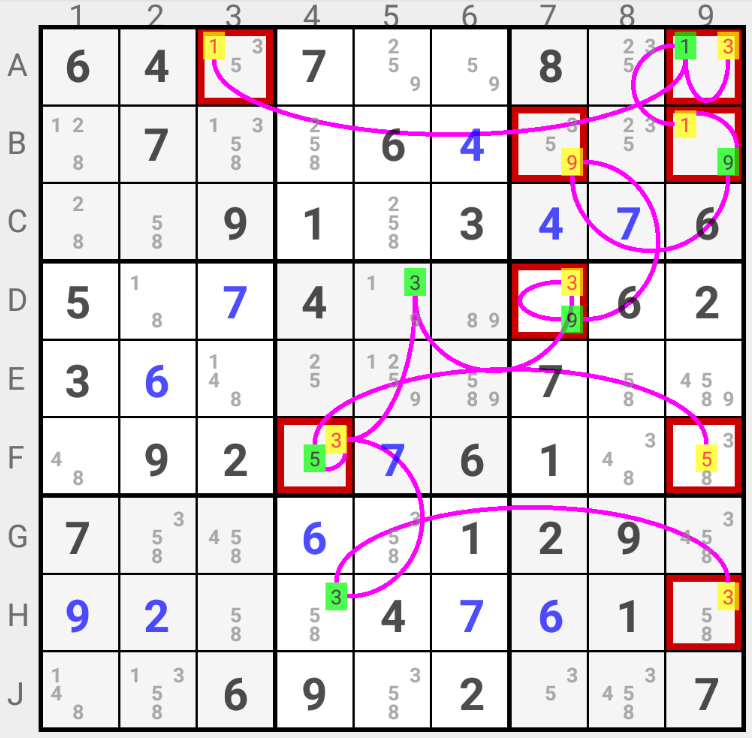
In the example, candidate 3 is colored in yellow in A9 and in H9. If the yellow color identified the solution, then candidate 3 would be the solution for two Cells in Column "9" which is impossible. Hence the green color identifies the solution and all candidates colored in yellow can be eliminated.

However this is a theoritical case. The chain is built using iterations. The iteration "coloring" the "second node" in the same unit is preceded by the iteration that has colored the linked node with the other color. Which means that during this preceding iteration, the "second node" already saw two candidates with differing colors (see below). In the example, before being colored in yellow, candidate 3 in H9 sees a yellow candidate 3 in A9 and a green candidate 3 in H4. Hence rule "3D MEDUSA (SEES TWO DIFFERENT COLORS)" would have been applied before coloring candidate 3 in H9 in yellow.

3D MEDUSA (TWO COLORS IN A CELL) : One of the two colors is the solution. If there are two candidates with different colors in a Cell, one of them must be the solution for that Cell. Hence all other candidates can be eliminated from the Cell.

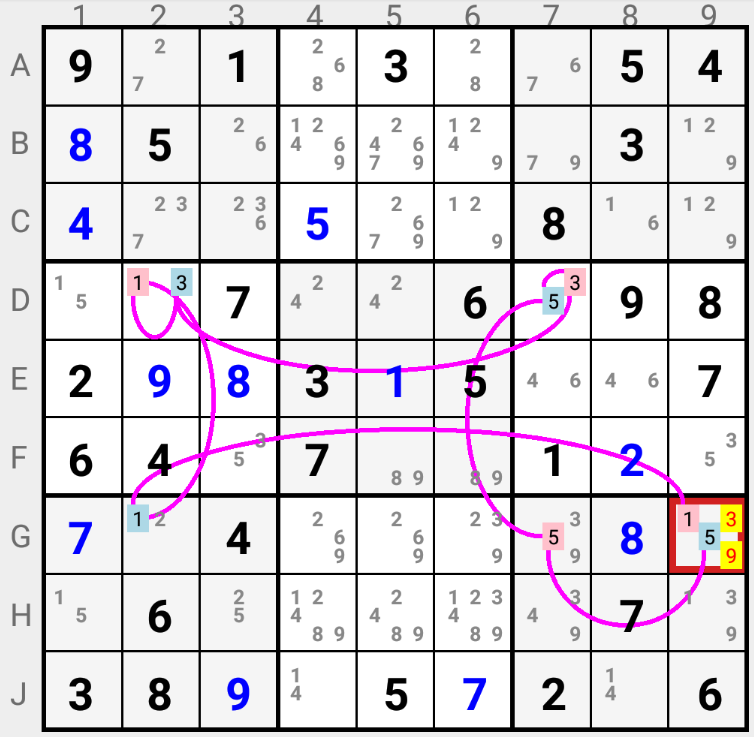
In the example G9 must have either candidate 1, or candidate 5, as solution. The other candidates in this Cell can not be the solution.

3D MEDUSA (SEES TWO DIFFERENT COLORS) : Either one, or the other, color is the solution. If an uncolored candidate can see two candidates of different colors, then it is eliminated by one of them (we do not know yet by which one).

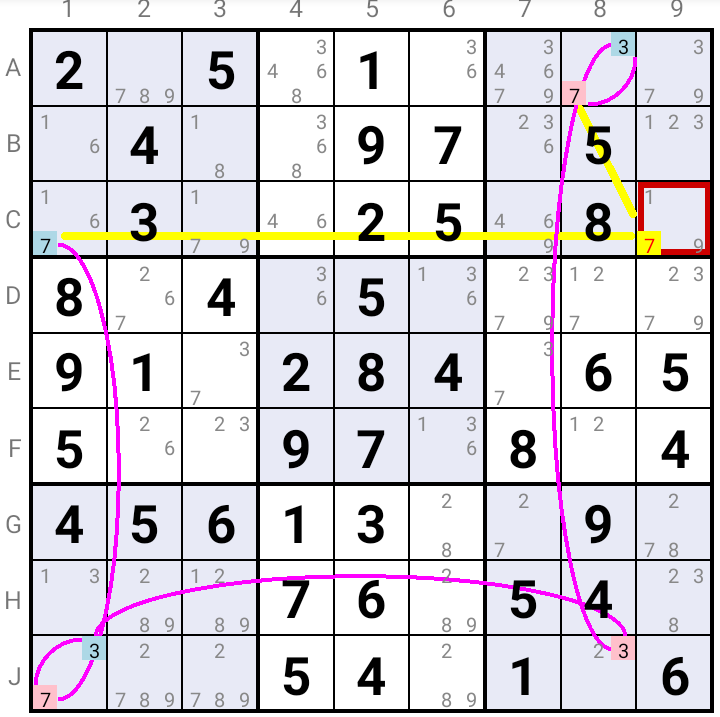
In the example, candidate 7 in C9 sees candidates 7 of different colors in A8 and in C1. As candidate 7 must be the solution in one of these cells, it can not be the solution in C9.

3D MEDUSA (UNIT-CELL ELIMINATION) : Either one, or the other, color is the solution. If an uncolored candidate can see a colored candidate with the same value and another candidate in its own Cell with the other color, then it can not be the solution and it can be eliminated.

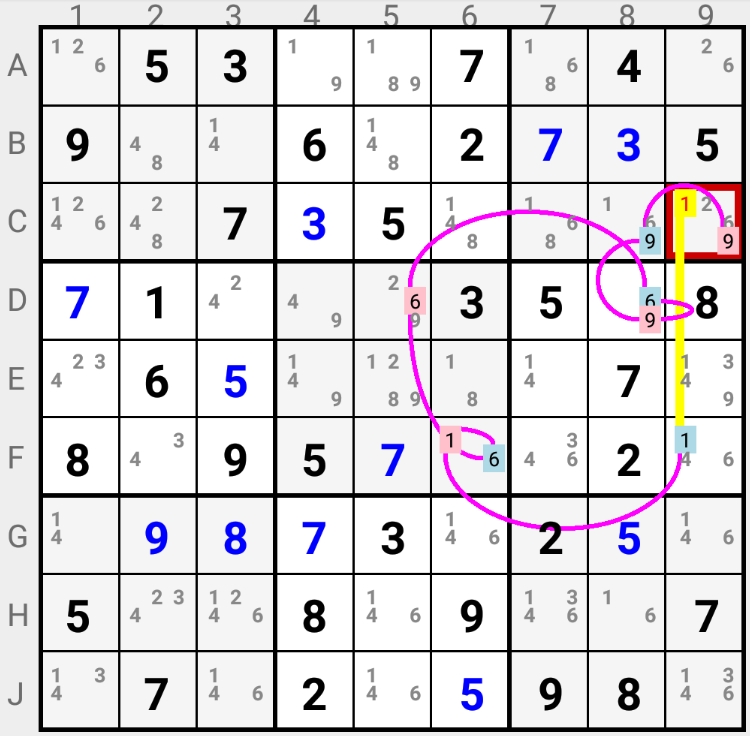
In the example either candidate 9 is the solution in C9, or candidate 1 is the solution in F9. As candidate 1 in C9 sees both candidates, it can not be the solution in C9.

3D MEDUSA (EMPTYING A CELL) : If a particular uncolored Cell can see Cells that each contain one of the candidates of the uncolored Cell and if all these candidates have the same color, then this color can not be the solution. Indeed, if it were the solution, it would eliminate all candidates from the particular Cell, which is not possible.

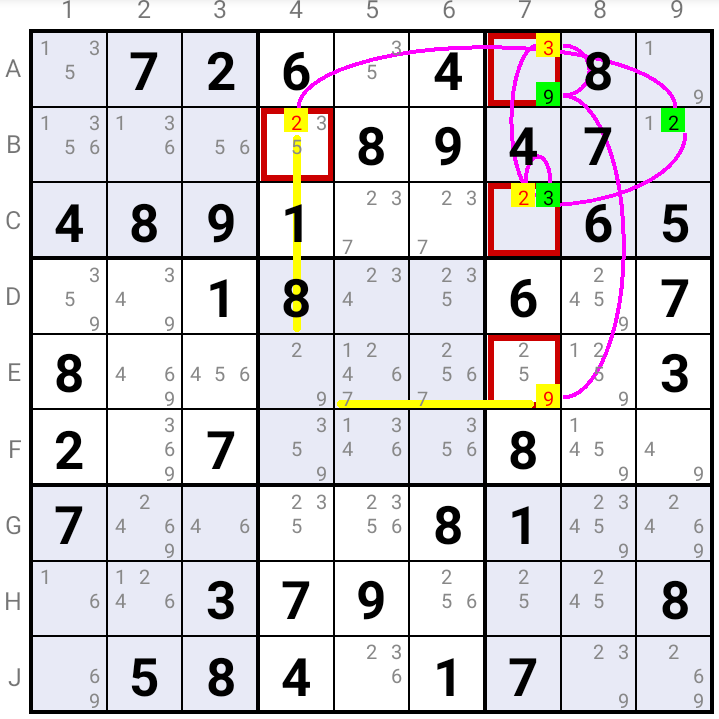
In the example if candidate 2 were the solution in B4 and candidate 9 the solution in E7, then all possible candidates would be eliminated in E4.

NB: more formally, a Strong Link is the relationship that exists between two Cells in a region (Row, Column or Square) when these two Cells are the only Cells in that region that contain a particular candidate: if the candidate is not the solution for the first Cell, then it must be the solution for the second Cell, and vice-versa.
However, in the Chaining Strategies, we consider Strong Links as links going from a Cell or a group of Cells where we assert the candidate is not the solution (we say the candidate is in the "OFF" state) to a Cell or a group of Cells where it then must be the solution (we say the candidate is in the "ON" state).
If we consider a Bi-Value Cell, asserting that one of its candidates is not the solution implies that the other candidate must be the solution. Hence there also exists a Strong Link between the two candidates of a "Bi-Value" Cell.

A Weak Link as a link going from a Cell/group of Cells where the candidate is "ON" to a Cell/group of Cells where it is "OFF".

You can practice this strategy by installing the SudokuCoach application on your Android™ device.